题目内容
12.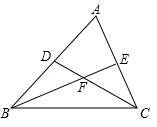 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,若∠BFC=116°,则∠A=( )
如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,若∠BFC=116°,则∠A=( )| A. | 51° | B. | 52° | C. | 53° | D. | 58° |
分析 根据角平分线的性质与三角形内角和性质即可求出∠A的值.
解答 解:由题意可知:∠FBC+∠FCB=180°-∠A=64°,
∵在△ABC中,∠B、∠C的平分线是BE,CD,
∴∠ABC+∠ACB=2(∠FBC+∠FCB)=128°,
∴∠A=180°-(∠ABC+∠ACB)=52°
故选(B)
点评 本题考查三角形内角和性质,解题的关键是根据角平分线的性质求出∠ABC+∠ACB的值,本题属于属于基础题型.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
20. 为进一步加强中小学生近视眼的防控工作,某地区教育主管部门对初二年级学生的视力进行了一次抽样调查,经数据分组整理,绘制的频数分布表与频数分布直方图的一部分如下(每组含前一个边界值,不含后一个边界值):
为进一步加强中小学生近视眼的防控工作,某地区教育主管部门对初二年级学生的视力进行了一次抽样调查,经数据分组整理,绘制的频数分布表与频数分布直方图的一部分如下(每组含前一个边界值,不含后一个边界值):
某地区初二学生视力抽样调查频数分布表
请根据以上信息解答下列问题:
(1)表中的a=60,b=0.30;
(2)在图中补全频数分布直方图;
(3)若视力在5.0以上(含5.0)均属正常,根据抽样调查数据,估计该地区6200名初二年级学生视力正常的有3100人.
 为进一步加强中小学生近视眼的防控工作,某地区教育主管部门对初二年级学生的视力进行了一次抽样调查,经数据分组整理,绘制的频数分布表与频数分布直方图的一部分如下(每组含前一个边界值,不含后一个边界值):
为进一步加强中小学生近视眼的防控工作,某地区教育主管部门对初二年级学生的视力进行了一次抽样调查,经数据分组整理,绘制的频数分布表与频数分布直方图的一部分如下(每组含前一个边界值,不含后一个边界值):某地区初二学生视力抽样调查频数分布表
| 分组 | 频数 | 频率 |
| 4.0~4.2 | 10 | 0.02 |
| 4.2~4.4 | 15 | 0.03 |
| 4.4~4.6 | 75 | 0.15 |
| 4.6~4.8 | a | 0.12 |
| 4.8~5.0 | 90 | 0.18 |
| 5.0~5.2 | 150 | b |
| 5.2~5.4 | 100 | 0.20 |
| 合计 | c | 1.00 |
(1)表中的a=60,b=0.30;
(2)在图中补全频数分布直方图;
(3)若视力在5.0以上(含5.0)均属正常,根据抽样调查数据,估计该地区6200名初二年级学生视力正常的有3100人.
7.下列从左到右的变形,( )是因式分解.
| A. | m(x-y)=mx-my | B. | -10m3-5m2+5m=-5m2(2m-1) | ||
| C. | 4+y2-4y=(y-2)2 | D. | m2-4-3m=(m+2)(m-2)-3m |
17.下列计算中:①$\sqrt{2}+\sqrt{3}$=$\sqrt{5}$,②2+$\sqrt{2}$=2$\sqrt{2}$;③3$\sqrt{2}$-$\sqrt{2}$=3;④3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$,正确的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
4.两位同学在解同一个方程组时,甲同学由$\left\{\begin{array}{l}{ax+by=9}\\{x+cy=11}\end{array}\right.$正确的解出$\left\{\begin{array}{l}{x=5}\\{y=3}\end{array}\right.$,乙同学因看错了c而解得$\left\{\begin{array}{l}{x=-1}\\{y=-6}\end{array}\right.$,那么a、b、c的正确的值为( )
| A. | a=3,b=-2,c=2 | B. | a=1,b=$\frac{4}{3}$,c=2 | C. | a=3,b=-2,c=-2 | D. | a=1,b=$\frac{4}{3}$,c=-2 |
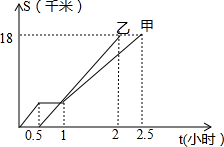 甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离 S(千米)和行驶时间t(小时)之间的关系图象如图2所示,根据图中提供的信息,有下列说法:
甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离 S(千米)和行驶时间t(小时)之间的关系图象如图2所示,根据图中提供的信息,有下列说法: