题目内容
5. 某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B篮球. C.羽毛球 D.乒乓球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B篮球. C.羽毛球 D.乒乓球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:(1)这次被调查的学生共有200人,在扇形统计图中“D”对应的圆心角的度数为72°;
(2)请你将条形统计图补充完整;
(3)在平时的羽毛球项目训练中,甲、乙、丙三人表现优秀,现决定从这三名同学中任选两名参加市里组织的羽毛球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
分析 (1)利用扇形统计图得到A类的百分比为10%,则用A类的频数除以10%可得到样本容量;然后用B类的百分比乘以360°得到在扇形统计图中“D”对应的圆心角的度数;
(2)先计算出C类的频数,然后补全统计图;
(3)画树状图展示所有12种等可能的结果,再找出恰好选中甲、乙两位同学的结果数,然后根据概率公式求解.
解答 解:(1)20÷$\frac{36°}{360°}$=200,
所以这次被调查的学生共有200人,
在扇形统计图中“D”对应的圆心角的度数=$\frac{40}{200}$×360°=72°;
故答案为200,72°;
(2)C类人数为200-80-20-40=60(人),
完整条形统计图为: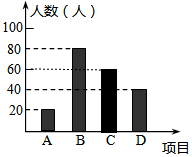
(3)画树状图得:
∵由上图可知,共有6种等可能的结果,其中恰好选中甲、乙两位同学的结果有2种.
所以P(恰好选中甲、乙两位同学)=$\frac{2}{6}$=$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.也考查了统计图.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
14.下列实数中,为无理数的是( )
| A. | 3.14 | B. | $\frac{22}{7}$ | C. | $\sqrt{3}$ | D. | $\sqrt{\frac{4}{9}}$ |
15.我县组织20辆汽车装运食品、药品、生活用品三种扶贫物资共100吨到某乡实施扶贫工作,按计划20辆汽车都要装运,每辆汽车只能装运同一种救灾物资且必须装满,根据表中提供的信息,解答下列问题:
(1)设装运食品的车辆数为x,装运药品的车辆数为y.求y与x的函数关系式;
(2)如果装运食品的车辆数不少于5辆,装运药品的车辆数不少于4辆,那么车辆的安排有几种方案?并写出每种安排方案;
(3)在(2)的条件下,若要求总运费最少,应如何安排车辆?并求出最少总运费.
| 物资种类 | 食品 | 药品 | 生活用品 |
| 每辆汽车运载量(吨) | 6 | 5 | 4 |
| 每吨所需运费(元/吨) | 120 | 160 | 100 |
(2)如果装运食品的车辆数不少于5辆,装运药品的车辆数不少于4辆,那么车辆的安排有几种方案?并写出每种安排方案;
(3)在(2)的条件下,若要求总运费最少,应如何安排车辆?并求出最少总运费.
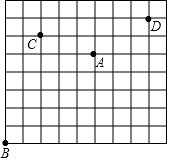 某水库的景区示意图如图所示(网格中每个小正方形的边长为1).若景点A的坐标为(3,3),请在图中画出相应的平面直角坐标系,并写出景点B、C、D的坐标.
某水库的景区示意图如图所示(网格中每个小正方形的边长为1).若景点A的坐标为(3,3),请在图中画出相应的平面直角坐标系,并写出景点B、C、D的坐标.