题目内容
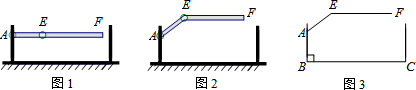
6. 如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE,∠E=36°,则∠ADC的度数是54°.
如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE,∠E=36°,则∠ADC的度数是54°.
分析 首先根据直径所对的圆周角是直角,可得∠BAE=90°,然后用90°减去∠E,求出∠B等于多少度;最后根据平行四边形的对角相等,可得∠ADC=∠B,据此解答即可.
解答 解:∵BE是直径,
∴∠BAE=90°,
∵∠E=36°,
∴∠B=90°-∠E=90°-36°=54°,
又∵∠ADC=∠B,
∴∠ADC=54°.
故答案为:54°.
点评 (1)此题主要考查了圆周角定理的应用,要熟练掌握,解答此题的关键是要明确:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
(2)此题还考查了平行四边形的性质的应用,要熟练掌握,解答此题的关键是要明确平行四边形的性质:①边:平行四边形的对边相等.②角:平行四边形的对角相等.③对角线:平行四边形的对角线互相平分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.2cos60°的值是( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
11.下列实数中,是有理数的为( )
| A. | $\sqrt{3}$ | B. | $\frac{1}{21}$ | C. | sin45° | D. | π |
18.在实数-0.8,2015,-$\frac{22}{7}$,$\frac{\sqrt{3}}{3}$四个数中,是无理数的是( )
| A. | -0.8 | B. | 2015 | C. | -$\frac{22}{7}$ | D. | $\frac{\sqrt{3}}{3}$ |
 如图所示,在△ABC中,AB=AC,CD垂直于BA的延长线于点D,试探究∠BAC与∠BCD之间的关系.
如图所示,在△ABC中,AB=AC,CD垂直于BA的延长线于点D,试探究∠BAC与∠BCD之间的关系.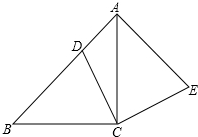 如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.