题目内容
16.已知关于x的一元二次方程x2+3x+m=0.(1)当m=4时,判断方程根的情况;
(2)当m=-4时,求方程的根.
分析 (1)当m=4时,方程化为x2+3x+4=0,然后计算判别式的值,根据判别式的意义判断方程根的情况;
(2)当m=-4时,方程化为x2+3x-4=0,然后利用因式分解法解方程.
解答 解:(1)当m=4时,方程化为x2+3x+4=0,
∵△=32-4×1×4=-7<0,
∴方程无实数根;
(2)当m=-4时,方程化为x2+3x-4=0,
(x+4)(x-1)=0,
所以x1=-4,x2=1.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了利用因式分解法解一元二次方程.

练习册系列答案
相关题目
11.不等式组$\left\{\begin{array}{l}{-2x<6}\\{2-x<0}\end{array}\right.$的解集是( )
| A. | x<-3 | B. | x>-3 | C. | x<2 | D. | x>2 |
5.若一次函数y=2mx+(m2-2m)的图象经过坐标原点,则( )
| A. | m=0或m=2 | B. | m=0 | C. | m=2 | D. | 无法确定 |
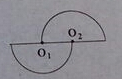 如图,⊙O1、⊙O2分别是两个半圆的圆心,这个圆形是中心对称图形吗?如果是,请指出对称中心;如果不是,请说明理由.
如图,⊙O1、⊙O2分别是两个半圆的圆心,这个圆形是中心对称图形吗?如果是,请指出对称中心;如果不是,请说明理由. 如图,一张纸上有A、B、C、D四个点,请找出一点M,使得MA=MB,MC=MD.
如图,一张纸上有A、B、C、D四个点,请找出一点M,使得MA=MB,MC=MD.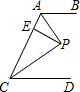 如图,AB∥CD,AP、CP分别是∠BAC和∠ACD的平分线,PE⊥AC于E,且PE=5cm,则AB与CD之间的距离是10cm.
如图,AB∥CD,AP、CP分别是∠BAC和∠ACD的平分线,PE⊥AC于E,且PE=5cm,则AB与CD之间的距离是10cm. 如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE,∠E=36°,则∠ADC的度数是54°.
如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE,∠E=36°,则∠ADC的度数是54°.