题目内容
1.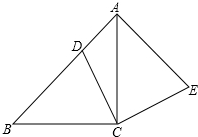 如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.(1)求证:AB⊥AE.
(2)若点D为AB中点,求证:四边形ADCE是正方形.
分析 (1)根据题意得出∠BCD=∠ACE,进而利用SAS得出△CBD≌△CAE求出即可;
(2)利用等腰直角三角形的性质得出∠ADC=90°,再得出四边形ADCE是矩形,结合正方形的判定方法得出即可.
解答 (1)解:∵∠ACB=90°,
∴∠BCD+∠ACD=90°,
∵∠DCE=90°,∴∠ACD+∠ACE=90°,
∴∠BCD=∠ACE,
在△CBD与△CAE中,∵$\left\{\begin{array}{l}{CB=CA}\\{∠BCD=∠ACE}\\{CD=CE}\end{array}\right.$,
∴△CBD≌△CAE(SAS),
∴∠B=∠CAE,
∵∠B+∠BAC=90°,∴∠BAC+∠EAC=90°,∴AB⊥AE;
(2)证明:∵点D为AB中点,
∴∠ADC=90°,
∵∠DCE=90°,∠BAE=90°,
∴四边形ADCE是矩形,
∴CD=CE,∴四边形ADCE是正方形.
点评 此题主要考查了正方形的判定以及全等三角形的判定与性质等知识,得出∠BCD=∠ACE是解题关键.

练习册系列答案
相关题目
11.不等式组$\left\{\begin{array}{l}{-2x<6}\\{2-x<0}\end{array}\right.$的解集是( )
| A. | x<-3 | B. | x>-3 | C. | x<2 | D. | x>2 |
13.方程$\frac{4}{x}$=$\frac{3}{x-2}$的解为( )
| A. | x=0 | B. | x=2 | C. | x=4 | D. | x=8 |
10.一根头发丝的直径约为0.00 006纳米,用科学记数法表示0.00 006,正确的是( )
| A. | 6×10-6 | B. | 6×10-5 | C. | 6×10-4 | D. | 0.6×10-4 |
11.已知三角形两边长分别为3和9,则此三角形的第三边的长可能是( )
| A. | 4 | B. | 5 | C. | 11 | D. | 15 |
 如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE,∠E=36°,则∠ADC的度数是54°.
如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE,∠E=36°,则∠ADC的度数是54°.