题目内容
7.根据下列条件分别求二次函数的表达式.(1)已知二次函数的图象经过点(-2,-1),且当x=-1时,函数有最大值2.
(2)已知二次函数图象的对称轴是直线x=1,与坐标轴交于点(0,-1),(-1,0).
分析 (1)由二次函数当x=-1时,有最大值是2,得到二次函数的顶点坐标为(-1,2),设出二次函数的顶点式方程,将(-2,-1)代入求出a的值,即可求出二次函数的解析式.
(2)已知抛物线的对称轴,可以设出函数的解析式是y=a(x-1)2+k,把(0,-1),(-1,0)代入函数解析式即可求得函数解析式.
解答 解:(1)由二次函数当x=-1时,有最大值是2,得到顶点坐标为(-1,2),
设二次函数解析式为y=a(x+1)2+2(a≠0),
将点(-2,-1)代入得:-1=a+2,
解得:a=-3,
则二次函数解析式为y=-3(x+1)2+2.
(2)设函数的解析式是y=a(x-1)2+k,根据题意得:
$\left\{\begin{array}{l}{a+k=-1}\\{4a+k=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{k=-\frac{4}{3}}\end{array}\right.$.
则函数的解析式是y=$\frac{1}{3}$(x-1)2-$\frac{4}{3}$.
点评 本题主要考查了待定系数法求二次函数的解析式,根据条件正确设出函数的解析式形式是解题的关键.

练习册系列答案
相关题目
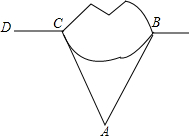 一个工程队在修路时要开挖一条笔直的隧道,如图所示,经测定,点B、C、D在同一条直线上,为加快施工进度,要在B、C两端同时施工,现在山外一点A(可直达B、C两点)测得∠A=55°,∠ACD=105°.问:在B点的施工队应按与BA成多少度角的方向施工,隧道才能在山中顺利接通?为什么?
一个工程队在修路时要开挖一条笔直的隧道,如图所示,经测定,点B、C、D在同一条直线上,为加快施工进度,要在B、C两端同时施工,现在山外一点A(可直达B、C两点)测得∠A=55°,∠ACD=105°.问:在B点的施工队应按与BA成多少度角的方向施工,隧道才能在山中顺利接通?为什么?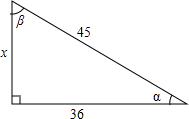 如图,分别求∠α和∠β的正弦、余弦和正切.
如图,分别求∠α和∠β的正弦、余弦和正切.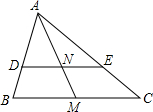 如图,△ABC中,AM为BC边上的中线,DE∥BC,求证:DN=NE.
如图,△ABC中,AM为BC边上的中线,DE∥BC,求证:DN=NE.