题目内容
已知,如图,在Rt△ABC中,∠C=90º,∠BAC的角平分线AD交BC边于D.
(1)以AB边上一点O为圆心,过A,D两点作⊙O(不写作法,保留作图痕迹),再判断直线BC与⊙O的位置关系,并说明理由;(2分+4分)
(2)若(1)中的⊙O与AB边的另一个交点为E,AB=6,BD=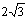 ,
,
求⊙O的半径.(4分)
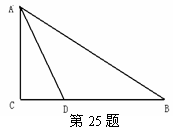
(1)如图,作AD的垂直平分 线交AB于点O,O为圆心,OA为半径作圆。
线交AB于点O,O为圆心,OA为半径作圆。


判断结果:BC是⊙O的切线。连结OD。
∵AD平分∠BAC ∴∠DAC=∠DAB
∵OA=OD ∴∠ODA=∠DAB
∴∠DAC=∠ODA ∴OD∥AC ∴∠ODB=∠C
∵∠C=90º ∴∠ODB=90º 即:OD⊥BC
∵OD是⊙O的半径 ∴ BC是⊙O的切线。
( 2) 如图,连结DE。
2) 如图,连结DE。
设⊙O的半径为r,则OB=6-r,
在Rt△ODB中,∠ODB=90º,
∴ 0B2=OD2+BD2 即:(6-r)2= r2+( )2
)2
∴r=2

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目

 背面图案相同的卡片A、B、C、D,其正面分别画有四个不同的几何图形(如图),小刚同学将这四张
背面图案相同的卡片A、B、C、D,其正面分别画有四个不同的几何图形(如图),小刚同学将这四张 卡片背面朝上洗匀
卡片背面朝上洗匀
 +
+ =0的根( )
=0的根( ) ,x2=-
,x2=- 的值为( )
的值为( ) D.
D.
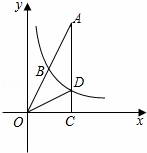
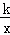 (k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .