题目内容
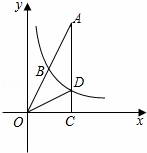
如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=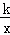 (k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
y=2x .
解:设OC=a,
∵点D在y= 上,
上,
∴CD= ,
,
∵△OCD∽△ACO,
∴ =
= ,
,
∴AC= =
= ,
,
∴点A(a, ),
),
∵点B是OA的中点,
∴点B的坐标为( ,
, ),
),
∵点B在反比例函数图象上,
∴ =
= ,
,
∴ =2k2,
=2k2,
∴a4=4k2,
解得,a2=2k,
∴点B的坐标为( ,a),
,a),
设直线OA的解析式为y=mx,
则m• =a,
=a,
解得m=2,
所以,直线OA的解析式为y=2x.
故答案为:y=2x.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
 ,
,
 -1)米,则需要安装闪光灯:
-1)米,则需要安装闪光灯:



