题目内容
已知二次函数y=a（x+2）2+b有最大值，当x=-3，-2，0时的函数值依次记作y1，y2，y3，则y1，y2，y3大小关系为 ．
考点：二次函数图象上点的坐标特征
专题：计算题
分析：根据二次函数的性质得a＜0，再分别计算出y1，y2，y3的值，然后比较代数式值的大小即可．
解答：解：∵二次函数y=a（x+2）2+b有最大值，
∴抛物线开口向下，
∴a＜0，
当x=-3时，y1=a（x+2）2+b=a+b；当x=-2时，y2=a（x+2）2+b=b；当x=0时，y3=a（x+2）2+b=4a+b，
∴y3＜y1＜y2．
故答案为y3＜y1＜y2．
∴抛物线开口向下，
∴a＜0，
当x=-3时，y1=a（x+2）2+b=a+b；当x=-2时，y2=a（x+2）2+b=b；当x=0时，y3=a（x+2）2+b=4a+b，
∴y3＜y1＜y2．
故答案为y3＜y1＜y2．
点评：本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．也考查了二次函数的性质和代数式值的大小比较．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
若有理数a，b，c在数轴上的位置如图所示，在下列结论中：①a-b＞0②ab＜0③a+b＜0④b（a-c）＞0，其中正确的个数有（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
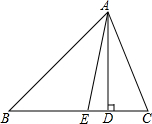如果，在△ABC中，AD是高，AE是∠BAC的平分线，∠BAC=54°，∠C=70°．求∠EAD的度数．