题目内容
 有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC,用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r= .
有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC,用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r= .
【答案】分析:连接OA,作OD⊥AB于点D,利用三角函数以及垂径定理即可求得AB的长,然后利用扇形的弧长公式即可求得弧长,然后利用圆的周长公式即可求得半径.
解答: 解:连接OA,作OD⊥AB于点D.
解:连接OA,作OD⊥AB于点D.
则∠DAO= ×60°=30°,OD=2,
×60°=30°,OD=2,
则AD= OD=
OD= ,
,
∴AB=2 .
.
则扇形的弧长是: =
= ,
,
根据题意得:2πr= ,
,
解得:r= .
.
故答案是: .
.
点评:本题考查了扇形的弧长公式,垂径定理,正确求得AB的长是关键.
解答:
 解:连接OA,作OD⊥AB于点D.
解:连接OA,作OD⊥AB于点D.则∠DAO=
 ×60°=30°,OD=2,
×60°=30°,OD=2,则AD=
 OD=
OD= ,
,∴AB=2
 .
.则扇形的弧长是:
 =
= ,
,根据题意得:2πr=
 ,
,解得:r=
 .
.故答案是:
 .
.点评:本题考查了扇形的弧长公式,垂径定理,正确求得AB的长是关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
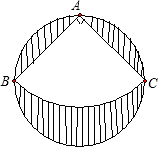 如图,有一直径为1m的圆形铁皮,要从中剪出一个最大的圆心角是90°的扇形ABC
如图,有一直径为1m的圆形铁皮,要从中剪出一个最大的圆心角是90°的扇形ABC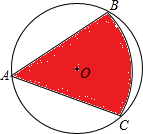 如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.那么剪下的扇形ABC(阴影部分)的面积为
如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.那么剪下的扇形ABC(阴影部分)的面积为 如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.那么剪下的扇形ABC(阴影部分)的面积为
如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.那么剪下的扇形ABC(阴影部分)的面积为