��Ŀ����
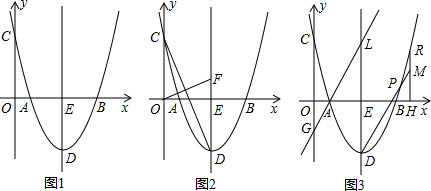
7�� ��ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ���ԭ��O����x���ཻ�ڵ�B��-4��0��������ΪD��ֱ��y=-x����κ�����ͼ���ڵ�A��m��8����ֱ��AD��x���ڵ�E����y���ڵ�F��
��ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ���ԭ��O����x���ཻ�ڵ�B��-4��0��������ΪD��ֱ��y=-x����κ�����ͼ���ڵ�A��m��8����ֱ��AD��x���ڵ�E����y���ڵ�F����1����m��ֵ�����κ����Ľ���ʽ��
��2����tan��AEB��ֵ��
��3����P������OA�ϵĶ��㣨��P���A��O���غϣ�������P��y���ƽ���߽����κ�����ͼ���ڵ�M���ʣ��Ƿ���ڵ�P��ʹ��P��A��MΪ��������������AOF���ƣ�������ڣ������P�����ꣻ��������ڣ���˵�����ɣ�
���� ��1�����ɶ��κ���y=ax2+bx+c��a��0����ͼ���ԭ��O���ó�c=0����y=ax2+bx�������A�����꣬Ȼ��A����B���������y=ax2+bx�����ô���ϵ��������������κ����Ľ���ʽ��
��2���������䷽�������κ���һ��ʽ��Ϊ����ʽ���������D�����꣬�����ô���ϵ�������ֱ��AD�Ľ���ʽ���������E�����꣬Ȼ����AG��x����G����ֱ�ǡ�AGE���������к����Ķ��弴�����tan��AEB��ֵ��
��3�����P������Ϊ��x��-x�������M������Ϊ��x��$\frac{1}{4}$x2+x��������������������ۣ��ٵ�-8��x��0ʱ�������APM�ס�AOF����Ȼ��M���D�غϣ������P������Ϊ��-2��2���������APM�ס�FOA���������������ζ�Ӧ�ߵı���ȵõ�$\frac{PM}{OA}$=$\frac{AP}{FO}$����$\frac{-x-\frac{1}{4}{x}^{2}-x}{8\sqrt{2}}$=$\frac{\sqrt{2}��x+8��}{4}$���ⷽ�̼��ɣ��ڵ�x��-8ʱ�����ڡ�APM=��FOA=135�㣬��MAP����OAF������ֻ�ܡ�APM�ס�FOA���������������ζ�Ӧ�ߵı�����г����̣�������⣮
��� �⣺��1���߶��κ���y=ax2+bx+c��a��0����ͼ���ԭ��O��
��c=0��
��y=ax2+bx��
��ֱ��y=-x����A��m��8����
��8=-m��m=-8��
��A��-8��8����
�߶��κ���y=ax2+bx��a��0����ͼ�����A��-8��8����B��-4��0����
��$\left\{\begin{array}{l}{64a-8b=8}\\{16a-4b=0}\end{array}\right.$�����$\left\{\begin{array}{l}{a=\frac{1}{4}}\\{b=1}\end{array}\right.$��
����κ����Ľ���ʽΪy=$\frac{1}{4}$x2+x�� ��2����y=$\frac{1}{4}$x2+x=$\frac{1}{4}$��x+2��2-1��
��2����y=$\frac{1}{4}$x2+x=$\frac{1}{4}$��x+2��2-1��
�ඥ��D������Ϊ��-2��-1����
��ֱ��AD�Ľ���ʽΪy=mx+n��
��A��-8��8����D��-2��-1����
��$\left\{\begin{array}{l}{-8m+n=8}\\{-2m+n=-1}\end{array}\right.$�����$\left\{\begin{array}{l}{m=-\frac{3}{2}}\\{n=-4}\end{array}\right.$��
��ֱ��AD�Ľ���ʽΪy=-$\frac{3}{2}$x-4��
��y=0ʱ��-$\frac{3}{2}$x-4=0�����x=-$\frac{8}{3}$��
��E��������-$\frac{8}{3}$��0����
��AG��x����G����AG=8��EG=-$\frac{8}{3}$-��-8��=$\frac{16}{3}$�� ��tan��AEB=$\frac{AG}{EG}$=$\frac{8}{\frac{16}{3}}$=$\frac{3}{2}$��
��tan��AEB=$\frac{AG}{EG}$=$\frac{8}{\frac{16}{3}}$=$\frac{3}{2}$��
��3�����P��������x��-x�������M��������x��$\frac{1}{4}$x2+x����
������������ۣ�
�ٵ�-8��x��0ʱ��
�����APM�ס�AOF����ô��M���D�غϣ���ʱx=-2�����P������Ϊ��-2��2����
�����APM�ס�FOA����ô$\frac{PM}{OA}$=$\frac{AP}{FO}$����$\frac{-x-\frac{1}{4}{x}^{2}-x}{8\sqrt{2}}$=$\frac{\sqrt{2}��x+8��}{4}$��
������x2+24x+128=0�� ���x1=-16��x2=-8��������������ȥ��
���x1=-16��x2=-8��������������ȥ��
�ڵ�x��-8ʱ��
�ߡ�APM=��FOA=135�㣬��MAP����OAF��
��ֻ�ܡ�APM�ס�FOA��
��$\frac{PM}{OA}$=$\frac{AP}{FO}$����$\frac{\frac{1}{4}{x}^{2}+x-��-x��}{8\sqrt{2}}$=$\frac{-\sqrt{2}��x+8��}{4}$��
������x2+24x+128=0��
���x1=-16��x2=-8������������ȥ����
���P��������-16��16����
���������������P��������-2��2����-16��16����
���� �����Ƕ��κ������ۺ����ͣ������漰����֪ʶ�������ô���ϵ��������κ�����һ�κ����Ľ���ʽ�����κ��������ʣ�������Ǻ����Ķ��壬���������ε��ж������ʣ������йض�������ʱҪע����������������۽����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | 1��2 | B�� | 2��1 | C�� | 1��4 | D�� | 4��1 |
| A�� | 55�� | B�� | 65�� | C�� | 145�� | D�� | 165�� |
| A�� | 20�� | B�� | 80�� | C�� | 20���80�� | D�� | ����ȷ�� |
 ��ͼ����ƽ���ı���ABCD�У���E�DZ�AD���е㣬EC���Խ���BD�ڵ�F����EF��FC���ڣ�������
��ͼ����ƽ���ı���ABCD�У���E�DZ�AD���е㣬EC���Խ���BD�ڵ�F����EF��FC���ڣ�������| A�� | 3��2 | B�� | 3��1 | C�� | 1��1 | D�� | 1��2 |
| A�� | a2+a3=a5 | B�� | a6��a2=a3 | C�� | ��-a2��3=a6 | D�� | -2a•a2=-2a3 |