Question

17．已知E、F、G、H是四边形ABCD各边上的中点且AC=BD，则四边形EFGH的形状是菱形．

Answer 1

分析 根据三角形中位线的性质，可得EF与GH的关系，根据平行四边的判定，可得四边形EFGH的形状，根据菱形的判定，可得答案．

解答 解：如图：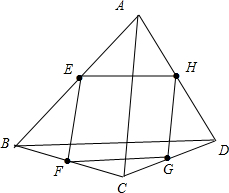
，
∵四边形ABCD中，E、F、G、H分别是四边的中点，
∴EF∥AC，HG∥AC，EF=$\frac{1}{2}$AC，GH=$\frac{1}{2}$AC，
∴EF∥HG，EF=GH，
∴EFGH是平行四边形．
同理FG=$\frac{1}{2}$AC．
∵AC=BD，
∴EF=FG，
∴四边形EFGH是菱形．
故答案是：菱形．

点评 本题考查了中点四边形，利用了三角形中位线的性质，平行四边形的判定，菱形的判定，注意四边形中点的图形是平行四边形，对角线相等的四边形中点的图形是菱形，对角线互相垂直的四边形中点的图形是矩形．