题目内容
甲、乙两人合做一项工程,4小时后甲因另有工作离开,剩下的工作由乙独做6小时完成.已知甲的工作效率是乙的工作效率二倍,问两人独做各需几小时?
考点:分式方程的应用
专题:
分析:设甲独做需要x小时完成此项工程,则乙独做需要2x小时完成此项工程,根据题意可得,甲4小时的任务+乙6小时完成的任务=1,据此列方程求解.
解答:解:设甲独做需要x小时完成此项工程,则乙独做需要2x小时完成此项工程,
由题意得,4(
+
)+6×
=1,
解得:x=9,
经检验,x=9是原分式方程的解,且符合题意,
则2x=18.
答:甲独做需要9小时完成此项工程,则乙独做需要18小时完成此项工程.
由题意得,4(
| 1 |
| x |
| 1 |
| 2x |
| 1 |
| 2x |
解得:x=9,
经检验,x=9是原分式方程的解,且符合题意,
则2x=18.
答:甲独做需要9小时完成此项工程,则乙独做需要18小时完成此项工程.
点评:本题考查了分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.

练习册系列答案
相关题目
下列各组中的两个图形,一定相似的是( )
| A、有一个角对应相等的两个菱形 |
| B、对应边成比例的两个多边形 |
| C、两条对角线对应成比例的两个平行四边形 |
| D、任意两个矩形 |
 有理数a、b在数轴上的位置如图所示,则下列各式中错误的是( )
有理数a、b在数轴上的位置如图所示,则下列各式中错误的是( )| A、b<0<a |
| B、|b|>|a| |
| C、a+b>0 |
| D、ab<0 |
 如图,已知AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
如图,已知AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O. 如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴上的一动点,连接CD,DE,以CD,DE为边作?CDEF.
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴上的一动点,连接CD,DE,以CD,DE为边作?CDEF.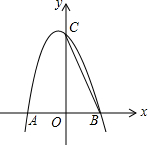 已知抛物线y=x2-2x+3经过B(1,0)、C(0,3),将直线BC向下平移,与抛物线交于点B′、C′(B′与B对应,C′与C对应),与y轴交于点D,当点D是线段B′C′的三等分点时,求点D的坐标.
已知抛物线y=x2-2x+3经过B(1,0)、C(0,3),将直线BC向下平移,与抛物线交于点B′、C′(B′与B对应,C′与C对应),与y轴交于点D,当点D是线段B′C′的三等分点时,求点D的坐标.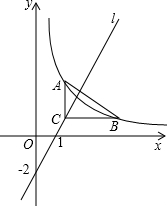 已知直线l经过点(1,0)(0,-2),Rt△ABC如图放置,其直角顶点C在直线l上,两直角边分别平行于坐标轴,AC=2,BC=3,将Rt△ABC沿直线l平移,使点A、B都在函数y=
已知直线l经过点(1,0)(0,-2),Rt△ABC如图放置,其直角顶点C在直线l上,两直角边分别平行于坐标轴,AC=2,BC=3,将Rt△ABC沿直线l平移,使点A、B都在函数y=