题目内容
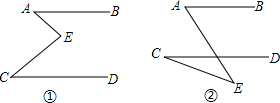 在图①和图②中,AB∥CD,你能说明∠A、∠E、∠C之间的大小关系吗?
在图①和图②中,AB∥CD,你能说明∠A、∠E、∠C之间的大小关系吗?考点:平行线的性质
专题:
分析:在①中过点E作EF∥AB,再结合平行线的性质可得到∠AEC=∠A+∠C;在②中设AE交CD于点F,根据平行线的性质和外角的性质可求得∠A、∠E、∠C之间的关系.
解答:解:
在①中过点E作EF∥AB,如图①,
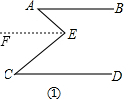
∵AB∥CD,
∴EF∥CD,
∴∠AEF=∠A,∠CEF=∠C,
∴∠AEC=∠A+∠C;
在②中设AE交CD于点F,如图②,
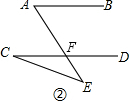
∵AB∥CD,
∴∠A=∠CFE,
又∠CFE=∠C+∠E,
∴∠A=∠C+∠E.
在①中过点E作EF∥AB,如图①,

∵AB∥CD,
∴EF∥CD,
∴∠AEF=∠A,∠CEF=∠C,
∴∠AEC=∠A+∠C;
在②中设AE交CD于点F,如图②,

∵AB∥CD,
∴∠A=∠CFE,
又∠CFE=∠C+∠E,
∴∠A=∠C+∠E.
点评:本题主要考查平行线的性质,掌握平行线的性质是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
下列各组数中,相等的一组是( )
| A、32与(-3)2 |
| B、23与(-2)3 |
| C、23与32 |
| D、-23与-32 |
三角形的三边长分别为5,1+2x,8,则x的取值范围是( )
| A、2<x<5 |
| B、2.5<x<4.5 |
| C、1<x<6 |
| D、3<x<5 |
下列单项式中,次数为5的是( )
| A、3a5b2 |
| B、-2a4b |
| C、-22a2b |
| D、4πa3b |
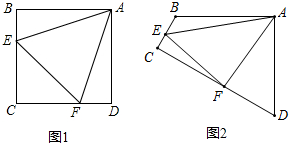
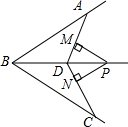 如图所示,BD是∠ABC的平分线,点P在射线BD上,PM⊥AD于M,PN⊥CD于N,PM=PN,求证:AB=CB.
如图所示,BD是∠ABC的平分线,点P在射线BD上,PM⊥AD于M,PN⊥CD于N,PM=PN,求证:AB=CB.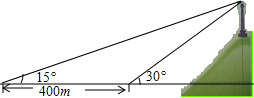 如图,小芳在山下发现正前方山上有个电视塔,测得塔尖的仰角为15°,小芳朝正前方笔直行走400m,此时测得塔尖的仰角为30°,若小芳的眼睛离地面1.6m,你能算出这个电视塔塔尖离地面的高度吗?
如图,小芳在山下发现正前方山上有个电视塔,测得塔尖的仰角为15°,小芳朝正前方笔直行走400m,此时测得塔尖的仰角为30°,若小芳的眼睛离地面1.6m,你能算出这个电视塔塔尖离地面的高度吗?