题目内容
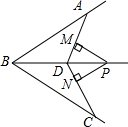 如图所示,BD是∠ABC的平分线,点P在射线BD上,PM⊥AD于M,PN⊥CD于N,PM=PN,求证:AB=CB.
如图所示,BD是∠ABC的平分线,点P在射线BD上,PM⊥AD于M,PN⊥CD于N,PM=PN,求证:AB=CB.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:根据PM⊥AD于M,PN⊥CD于N,PM=PN,易证∠ADB=∠CDB,从而证明△BAD≌△BCD,即可得出AB=CB.
解答:证明:∵PM⊥AD,PN⊥CD,PM=PN,
∴∠ADP=∠CDP,
∵∠ADB+∠ADP=180°,∠CDP+∠CDB=180°,
∴∠ADB=∠CDB,
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(ASA),
∴AB=CB.
∴∠ADP=∠CDP,
∵∠ADB+∠ADP=180°,∠CDP+∠CDB=180°,
∴∠ADB=∠CDB,
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
|
∴△ABD≌△CBD(ASA),
∴AB=CB.
点评:本题考查了全等三角形的性质和判定,角平分线性质的应用,解此题的关键是推出△ABD≌△CBD,注意:全等三角形的对应边相等.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
下列式子成立的是( )
| A、sin30°>sin60° |
| B、cos30°<cos60° |
| C、tan30°<tan60° |
| D、cos30°<sin30° |
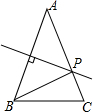 如图,△ABC中,AB=AC,AB的垂直平分线交AC于P点,若AB=5cm,BC=2cm,则△PBC的周长等于( )
如图,△ABC中,AB=AC,AB的垂直平分线交AC于P点,若AB=5cm,BC=2cm,则△PBC的周长等于( )| A、4cm | B、6cm |
| C、7cm | D、10cm |
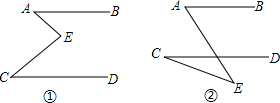 在图①和图②中,AB∥CD,你能说明∠A、∠E、∠C之间的大小关系吗?
在图①和图②中,AB∥CD,你能说明∠A、∠E、∠C之间的大小关系吗?