题目内容
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整并解答.
原题:(1)如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD 上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF.说明理由.
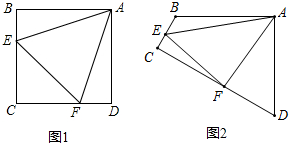
原题:(1)如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD 上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系

考点:全等三角形的判定与性质,旋转的性质
专题:
分析:(1)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,证出△AFG≌△AFE,根据全等三角形的性质得出EF=FG,即可得出答案;
(2)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,证出△AFE≌△AFG,根据全等三角形的性质得出EF=FG,即可得出答案.
(2)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,证出△AFE≌△AFG,根据全等三角形的性质得出EF=FG,即可得出答案.
解答:(1)解:理由是:如图1,

∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图1,
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线,
则∠DAG=∠BAE,AE=AG,
∠FAG=∠FAD+∠GAD=∠FAD+∠BAE=90°-45°=45°=∠EAF,
即∠EAF=∠FAG,
在△EAF和△GAF中,
,
∴△AFG≌△AFE(SAS),
∴EF=FG=BE+DF;
(2)解:∠B+∠D=180°时,EF=BE+DF;
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图2,

∴∠BAE=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠EAF=∠FAG,
∵∠ADC+∠B=180°,
∴∠FDG=180°,点F、D、G共线,
在△AFE和△AFG中,
∴△AFE≌△AFG(SAS),
∴EF=FG,
即:EF=BE+DF,
故答案为:∠B+∠ADC=180°.

∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图1,
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线,
则∠DAG=∠BAE,AE=AG,
∠FAG=∠FAD+∠GAD=∠FAD+∠BAE=90°-45°=45°=∠EAF,
即∠EAF=∠FAG,
在△EAF和△GAF中,
|
∴△AFG≌△AFE(SAS),
∴EF=FG=BE+DF;
(2)解:∠B+∠D=180°时,EF=BE+DF;
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图2,

∴∠BAE=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠EAF=∠FAG,
∵∠ADC+∠B=180°,
∴∠FDG=180°,点F、D、G共线,
在△AFE和△AFG中,
|
∴△AFE≌△AFG(SAS),
∴EF=FG,
即:EF=BE+DF,
故答案为:∠B+∠ADC=180°.
点评:本题考查了全等三角形的性质和判定,正方形的性质的应用,解此题的关键是能正确作出辅助线得出全等三角形,综合性比较强,有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列式子中一定是二次根式的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列式子成立的是( )
| A、sin30°>sin60° |
| B、cos30°<cos60° |
| C、tan30°<tan60° |
| D、cos30°<sin30° |
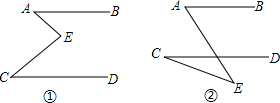 在图①和图②中,AB∥CD,你能说明∠A、∠E、∠C之间的大小关系吗?
在图①和图②中,AB∥CD,你能说明∠A、∠E、∠C之间的大小关系吗?