题目内容
(1)解方程:2x2-3x-2=0;
(2)解不等式组:
.
(2)解不等式组:
|
考点:解一元一次不等式组,解一元二次方程-因式分解法
专题:
分析:(1)方程可以变形成(x-2)(2x+1)=0,转化成一元一次方程即可求解;
(2)先求出不等式组中每一个不等式的解集,再求出它们的公共部分就是不等式组的解集.
(2)先求出不等式组中每一个不等式的解集,再求出它们的公共部分就是不等式组的解集.
解答:解:(1)原式即(x-2)(2x+1)=0,
则x-2=0或2x+1=0,
解得:x1=2,x2=-0.5;
(2)
,
解①得:x>2,
解②得:x<4.
则不等式组的解集是:2<x<4.
则x-2=0或2x+1=0,
解得:x1=2,x2=-0.5;
(2)
|
解①得:x>2,
解②得:x<4.
则不等式组的解集是:2<x<4.
点评:本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 如图,直线AB、CD相交于点O,∠AOD=80°,OE平分∠BOC,求∠AOE的度数.
如图,直线AB、CD相交于点O,∠AOD=80°,OE平分∠BOC,求∠AOE的度数.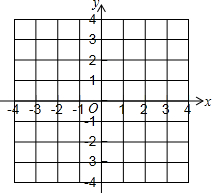 二次函数y=ax2+bx+c的图象过点(0,-3),(4,3),(2,-2).
二次函数y=ax2+bx+c的图象过点(0,-3),(4,3),(2,-2).
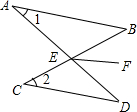 如图,AB∥CD,AD与BC交于点E,EF是∠BED的平分线,若∠1=29°,∠2=47°,则∠BEF=
如图,AB∥CD,AD与BC交于点E,EF是∠BED的平分线,若∠1=29°,∠2=47°,则∠BEF=