题目内容
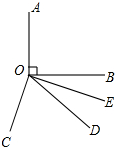 如图所示,OA⊥OB,OC⊥OE,OD为∠BOC的平分线,∠BOE=16°,求∠DOE的度数.
如图所示,OA⊥OB,OC⊥OE,OD为∠BOC的平分线,∠BOE=16°,求∠DOE的度数.考点:垂线,角平分线的定义
专题:
分析:首先根据垂直定义以及角平分线的性质得出∠BOD的度数,进而得出∠DOE的度数.
解答:解:∵OC⊥OE,
∴∠COE=90°,
∵∠BOE=16°,
∴∠COB=90°+16°=106°,
∵OD为∠BOC的平分线,
∴∠BOD=53°,
∴∠DOE=53°-16°=37°.
∴∠COE=90°,
∵∠BOE=16°,
∴∠COB=90°+16°=106°,
∵OD为∠BOC的平分线,
∴∠BOD=53°,
∴∠DOE=53°-16°=37°.
点评:此题主要考查了角平分线的性质以及垂直定义,正确求出∠COB的度数是解题关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
下列说法:
①全等三角形的形状相同、大小相等
②全等三角形的对应边相等、对应角相等
③面积相等的两个三角形全等
④全等三角形的周长相等
其中正确的说法为( )
①全等三角形的形状相同、大小相等
②全等三角形的对应边相等、对应角相等
③面积相等的两个三角形全等
④全等三角形的周长相等
其中正确的说法为( )
| A、①②③④ | B、①②③ |
| C、②③④ | D、①②④ |
方程x2+3x-9=0的负数解的范围( )
| A、-5<x<-4 |
| B、-4<x<-3 |
| C、-3<x<-2 |
| D、-2<x<0 |
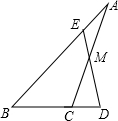 如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=
如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=| 1 |
| 4 |
| A、2:1 | B、3:2 |
| C、3:1 | D、5:2 |
