题目内容
非零整数m,n满足|m|+|n|=4,所有这样的整数组(m、n)共有 组.
考点:绝对值
专题:
分析:根据绝对值的意义,可得答案.
解答:解:非零整数满足|m|+|n|=4,
则|m|={1,2,3,},对应|n|={3,2,1},
当m=±1时,n=±3;
当m=±2时,n=±2;
当m=±3时,n=±1;
一共有12组.
故答案为:12.
则|m|={1,2,3,},对应|n|={3,2,1},
当m=±1时,n=±3;
当m=±2时,n=±2;
当m=±3时,n=±1;
一共有12组.
故答案为:12.
点评:本题考查里绝对值,利用了非零的绝对值都是正数.

练习册系列答案
相关题目
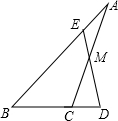 如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=
如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=| 1 |
| 4 |
| A、2:1 | B、3:2 |
| C、3:1 | D、5:2 |
小明和小华解同一个一元二次方程时,小明看错一次项系数,解得两根为2,-3,而小华看错常数项,解错两根为-2,5,那么原方程为( )
| A、x2-3x+6=0 |
| B、x2-3x-6=0 |
| C、x2+3x-6=0 |
| D、x2+3x+6=0 |

 某市在“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知AB=30m,AC=40m,∠BAC=150°,这种草皮每平方米售价a元,求购买这种草皮至少要多少元?
某市在“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知AB=30m,AC=40m,∠BAC=150°,这种草皮每平方米售价a元,求购买这种草皮至少要多少元?