题目内容
已知有理数a,b满足ab2<0,a+b>0,且|a|=2,|b|=3,求|
|+(b-1)2.
| a-1 |
| 3 |
考点:代数式求值
专题:
分析:根据有理数的乘法、有理数的加法,可得a、b的取值范围,根据绝对值的意义,可得a、b的值,根据代数式求值,可得答案.
解答:解:∵a,b满足ab2<0,a+b>0,且|a|=2,|b|=3,
∴a=-2,b=3.
把a=-2,b=3代入|
|+(b-1)2=|
|+(3-1)2=1+4=5.
∴a=-2,b=3.
把a=-2,b=3代入|
| a-1 |
| 3 |
| -2-1 |
| 3 |
点评:本题考查了代数式求值,确定a、b的值是解题关键.

练习册系列答案
相关题目
方程x2+3x-9=0的负数解的范围( )
| A、-5<x<-4 |
| B、-4<x<-3 |
| C、-3<x<-2 |
| D、-2<x<0 |
下列事件发生的概率为0的是( )
| A、随意掷一枚均匀的硬币两次,至少有一次反面朝上 |
| B、今年冬天黑龙江会下雪 |
| C、随意掷两个均匀的骰子,朝上面的点数之和为1 |
| D、一个转盘被分成6个扇形,按红、白、白、红、红、白排列,转动转盘,指针停在红色区域 |
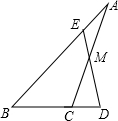 如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=
如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=| 1 |
| 4 |
| A、2:1 | B、3:2 |
| C、3:1 | D、5:2 |