题目内容
9.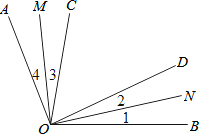 如图,已知∠AOB=120°,∠COD=50°,OM平分∠BOD,即∠1=∠2,ON平分∠AOC,即∠3=∠4;
如图,已知∠AOB=120°,∠COD=50°,OM平分∠BOD,即∠1=∠2,ON平分∠AOC,即∠3=∠4;(1)若∠BOD=30°,则∠MON=85°;
(2)若∠COD可以在∠AOB内部绕点O作任意旋转(射线OC与射线OA不重合,射线OD与射线OB不重合)则∠MON的大小是否改变?试说明理由.
分析 (1)由图形可知∠AOC=∠AOB-∠COD-∠BOD,由∠AOB=120°,∠COD=50°,∠BOD=30°,可得∠AOC的度数,再根据角平分线的定义可得∠2=$\frac{1}{2}$∠BOD,∠3=$\frac{1}{2}$∠AOC,再利用∠MON=∠COD+∠2+∠3,即可求得∠MON的度数;
(2)由题意知∠AOC+∠BOD=∠AOB-∠COD=120°-50°=70°,根据角平分线的定义可得∠2=$\frac{1}{2}$∠BOD,∠3=$\frac{1}{2}$∠AOC,所以∠2+∠3=$\frac{1}{2}$(∠AOC+∠BOD)=35°,故可得∠MON=∠COD+∠2+∠3=50°+35°=85°,故∠MON的大小不会改变.
解答 解:(1)∵∠AOB=120°,∠COD=50°,∠BOD=30°,
∴∠AOC=120°-50°-30°=40°,
∵OM平分∠BOD,即∠1=∠2,ON平分∠AOC,即∠3=∠4,
∴∠2=15°,∠3=20°,
∴∠MON=∠COD+∠2+∠3=50°+15°+20°=85°,
故答案为:85°;
(2)不改变,理由:
∵∠AOB=120°,∠COD=50°,
∴∠AOC+∠BOD=∠AOB-∠COD=120°-50°=70°,
∵OM平分∠BOD,即∠1=∠2,ON平分∠AOC,即∠3=∠4,
∴∠2=$\frac{1}{2}$∠BOD,∠3=$\frac{1}{2}$∠AOC,
∴∠2+∠3=$\frac{1}{2}$(∠AOC+∠BOD)=35°,
∴∠MON=∠COD+∠2+∠3=50°+35°=85°,
故不改变.
点评 本题主要考查了角平分线的定义,角的计算,掌握好角平分线的定义及角之间的和差关系是关键.

练习册系列答案
相关题目
14.某天同时同地,甲同学测得1m的测竿在地面上影长为0.8m,乙同学测得国旗旗杆在地面上的影长为9.6m,则国旗旗杆的长为( )
| A. | 10m | B. | 12m | C. | 13m | D. | 15m |
1.若等腰三角形的两边长分别是2和6,则这个三角形的周长是( )
| A. | 14 | B. | 10 | C. | 14或10 | D. | 以上都不对 |
19.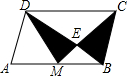 如图,已知M为平行四边形ABCD的边AB的中点,CM交BD于点E,BD=3BE,则图中阴影部分的面积与平行四边形ABCD面积的比是( )
如图,已知M为平行四边形ABCD的边AB的中点,CM交BD于点E,BD=3BE,则图中阴影部分的面积与平行四边形ABCD面积的比是( )
 如图,已知M为平行四边形ABCD的边AB的中点,CM交BD于点E,BD=3BE,则图中阴影部分的面积与平行四边形ABCD面积的比是( )
如图,已知M为平行四边形ABCD的边AB的中点,CM交BD于点E,BD=3BE,则图中阴影部分的面积与平行四边形ABCD面积的比是( )| A. | 1:2 | B. | 2:5 | C. | 3:5 | D. | 1:3 |
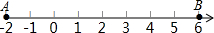 如图,数轴上A,B两点表示的数分别为-2和6,数轴上的点C是AB的中点,数轴上点D,使AD=$\frac{3}{2}$AC,则线段BD的长是2或14.
如图,数轴上A,B两点表示的数分别为-2和6,数轴上的点C是AB的中点,数轴上点D,使AD=$\frac{3}{2}$AC,则线段BD的长是2或14.
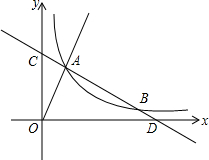 已知直线y=$\frac{1}{2}$x+$\frac{5}{2}$与反比例函数y=$\frac{m}{x}$图象相交于点A、B,OA⊥AB.
已知直线y=$\frac{1}{2}$x+$\frac{5}{2}$与反比例函数y=$\frac{m}{x}$图象相交于点A、B,OA⊥AB.