题目内容
如图，六边形ABCDEF中，AB∥DC，∠1、∠2、∠3、∠4分别是∠BAF、∠AFE、∠FED、∠EDC的外角，则∠1+∠2+∠3+∠4=考点：多边形内角与外角
专题：
分析：根据多边形的外角和减去∠B和∠C的外角的和即可确定四个外角的和．
解答：解：∵AB∥DC，
∴∠B+∠C=180°，
∴∠B与∠C的外角和为180°，
∵六边形ABCDEF的外角和为360°，
∴∠1+∠2+∠3+∠4=180°，
故答案为：180°．
∴∠B+∠C=180°，
∴∠B与∠C的外角和为180°，
∵六边形ABCDEF的外角和为360°，
∴∠1+∠2+∠3+∠4=180°，
故答案为：180°．
点评：本题考查了多边形的外角和定理，解题的关键是发现∠B和∠C的外角的和为180°，难度中等．
练习册系列答案
相关题目
如图，菱形ABCD中，∠DAB=60°，DF⊥AB于点E，且DF=DC，连接FC，则∠ACF的度数为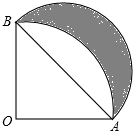
如图，扇形AOB的半径为1，∠AOB=90°，以AB为直径画半圆．则图中阴影部分的周长为