题目内容
设M=x2-8x+22,N=-x2-8x-3,是确定M与N的大小关系,并说明理由.
考点:整式的加减
专题:
分析:利用求差法判定两式的大小,将M与N代入M-N中,去括号合并得到最简结果,根据结果的正负即可做出判断.
解答:解:∵M=x2-8x+22,N=-x2-8x-3,
∴M-N=x2-8x+22-(-x2-8x-3)=x2-8x+22+x2+8x+3=2x2+25,
∵2x2≥0,
∴2x2+25>0,
∴M-N>0,
∴M>N.
∴M-N=x2-8x+22-(-x2-8x-3)=x2-8x+22+x2+8x+3=2x2+25,
∵2x2≥0,
∴2x2+25>0,
∴M-N>0,
∴M>N.
点评:此题考查了整式的加减,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
双曲线y=-
上两点为(x1,y1),(x2,y2),且x1<x2<0,则下列说法正确的是( )
| 2 |
| 3x |
| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、不能确定 |
 如图是在方格纸上画出的一个零件图形的一半,请你以过点M,N的直线为对称轴画出另一半.
如图是在方格纸上画出的一个零件图形的一半,请你以过点M,N的直线为对称轴画出另一半. 如图,△ABC中,AB=AC,D是BC边的中点,CE⊥AB于E.试说明:△ABD∽CBE.
如图,△ABC中,AB=AC,D是BC边的中点,CE⊥AB于E.试说明:△ABD∽CBE.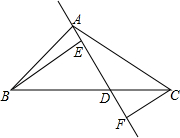 在△ABC中,AD是过A的一条射线,交BC于D,过B作BE⊥AD于E,过C作CF⊥AD于F.
在△ABC中,AD是过A的一条射线,交BC于D,过B作BE⊥AD于E,过C作CF⊥AD于F.