题目内容
3.如图1,在平面直角坐标系中,二次函数y=ax2-2x+2的图象与y轴交于点C,以OC为一边向左侧作正方形OCBA,点B刚好落在抛物线上.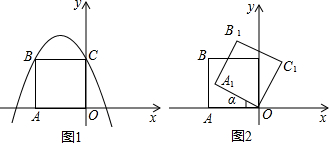
(1)求a的值;
(2)若点D在二次函数y=ax2-2x+2的图象的对称轴上,点E在二次函数y=ax2-2x+2的图象上,是否存在以B,C,D,E四点为顶点的四边形为平行四边形?若存在,请直接写出所有满足条件的点E坐标;若不存在,请说明理由.
(3)如图2,把正方形OCBA绕点O顺时针旋转α后得到正方形A1B1C1O(0°<α<90°).在旋转过程中,若点A1落在二次函数y=ax2-2x+2的图象对称轴上,求出此时的点B1的坐标.
分析 (1)先求出点C的坐标,再根据正方形的边长相等,得出点B的坐标,代入y=ax2-2x+2,即可得出a的值.
(2)分两种情况求解:①当点E在抛物线顶点时;②当BC∥DE,且DE=BC=2时,即可求出答案;
(3)由点A1落在二次函数对称轴上,OA1=2,可得出∠A1OA=60°,进而得出∠BOB1=60°,求出∠B1OC=15°,利用三角函数表示点B1的坐标即可.
解答 解:(1)二次函数y=ax2-2x+2的图象与y轴交于点C,
∴C(0,2),
∵以OC为一边向左侧作正方形OCBA,点B刚好落在抛物线上.
∴B(-2,2),把B(-2,2)代入y=ax2-2x+2,得2=4a+4+2,解得a=-1.
(2)①当点E在抛物线顶点时,
∵二次函数的解析式为y=-x2-2x+2.
∴E(-1,3)
∵点D在二次函数的对称轴上,
∴当E(-1,3)以B,C,D,E四点为顶点的四边形为平行四边形
②当BC∥DE,且DE=BC=2时,
∵点D在二次函数的对称轴上,
∴D的横坐标为-1,
∴设点E的横坐标为t,则有-1-t=2,或t-(-1)=2,解得t=-3或1.
∴E(-3,-1)或(1,-1)
综上所述:当点E的坐标为(-1,3)或(-3,-1)或(1,-1),以B,C,D,E四点为顶点的四边形为平行四边形.
(3)如图1,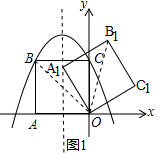
∵点A1落在二次函数对称轴上,OA1=2
∴∠A1OA=60°,
∴∠BOB1=60°,
∴∠B1OC=60°-45°=15°,
∵OB1=OB=2$\sqrt{2}$,
∴B1(2$\sqrt{2}$sin15°,2$\sqrt{2}$cos15°).
点评 本题主要考查了二次函数综合题,求二次函数图象与坐标轴的交点,正方形的性质,配方法,相似三角形的判定与性质,锐角三角函数,等腰直角三角形的性质,难点在于第(2)小题的两个小题都要分情况讨论,并且运算量较大.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案 一座抛物线型拱桥如图所示,桥下水面宽度是6m,拱高是3m,当水面上升1m后,水面的宽度是多少?(结果精确到0.1m)
一座抛物线型拱桥如图所示,桥下水面宽度是6m,拱高是3m,当水面上升1m后,水面的宽度是多少?(结果精确到0.1m)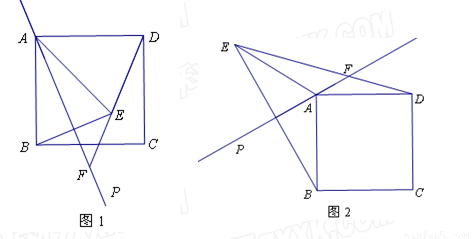
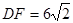 ,
,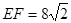 ,求线段AF的长.
,求线段AF的长.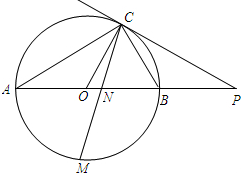 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.