题目内容
15.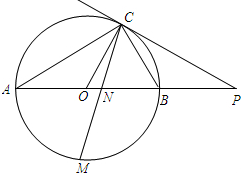 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.(1)求证:PC是⊙O的切线;
(2)点M是弧AB的中点,连MA,MB,CM交AB于点N,若AB=4,求MN•MC的值.
分析 (1)已知C在圆上,故只需证明OC与PC垂直即可;根据圆周角定理,易得∠PCB+∠OCB=90°,即OC⊥CP;故PC是⊙O的切线;
(2)连接MA,MB,由圆周角定理可得∠ACM=∠BCM,进而可得△MBN∽△MCB,故BM2=MN•MC;代入数据可得MN•MC=BM2=8.
解答 (1)证明:∵OA=OC,
∴∠A=∠ACO.
又∵∠COB=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
又∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°,OC⊥CP.
∵OC是⊙O的半径,
∴PC是⊙O的切线.
(2)解:连接MA,MB,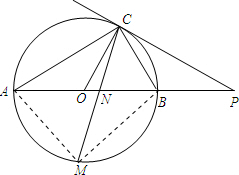
∵点M是$\widehat{AB}$的中点,
∴$\widehat{AM}=\widehat{BM}$.
∴∠ACM=∠BCM.
∵∠ACM=∠ABM,
∴∠BCM=∠ABM.
∵∠BMN=∠BMC,
∴△MBN∽△MCB.
∴$\frac{BM}{MC}$=$\frac{MN}{BM}$.
∴BM2=MN•MC.
又∵AB是⊙O的直径,$\widehat{AM}$=$\widehat{BM}$,
∴∠AMB=90°,AM=BM.
∵AB=4,
∴BM=2$\sqrt{2}$.
∴MN•MC=BM2=8.
点评 此题主要考查圆的切线的判定及圆周角定理的运用和相似三角形的判定和性质的应用,证得BM2=MN•MC是解题的关键.

练习册系列答案
相关题目
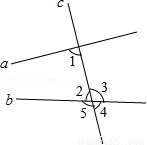
10. 如图,将含30°角的三角板的直角顶点放在直尺的一边上,若∠1=40°,则∠2的度数为( )
如图,将含30°角的三角板的直角顶点放在直尺的一边上,若∠1=40°,则∠2的度数为( )
 如图,将含30°角的三角板的直角顶点放在直尺的一边上,若∠1=40°,则∠2的度数为( )
如图,将含30°角的三角板的直角顶点放在直尺的一边上,若∠1=40°,则∠2的度数为( )| A. | 90° | B. | 80° | C. | 75° | D. | 70° |
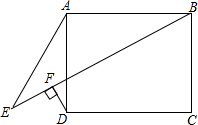 如图,矩形ABCD.AE=CD,DF⊥BE于F.求证:∠E=∠ADF.
如图,矩形ABCD.AE=CD,DF⊥BE于F.求证:∠E=∠ADF. a、b在数轴上的位置如图所示(用等号或不等号填空),则a+b<0;a-b>0.
a、b在数轴上的位置如图所示(用等号或不等号填空),则a+b<0;a-b>0.