题目内容
12.解下列方程:(1)$\frac{1}{x}=\frac{5}{x+3}$;
(2)$\frac{x}{x-1}=\frac{3}{2x-2}-2$;
(3)$\frac{2}{2x-1}=\frac{4}{4{x}^{2}-1}$;
(4)$\frac{3}{{x}^{2}+2x}-\frac{1}{{x}^{2}-2x}=0$;
(5)$\frac{x}{x-3}=\frac{x+1}{x-1}$;
(6)$\frac{x-3}{x-2}+1=\frac{3}{2-x}$;
(7)$\frac{2x+1}{{x}^{2}+x}=\frac{5}{6x+6}$;
(8)$\frac{3}{2}-\frac{1}{3x-1}=\frac{5}{6x-2}$.
分析 各分式方程乘以最简公分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:x+3=5x,
解得:x=$\frac{3}{4}$,
经检验x=$\frac{3}{4}$是分式方程的解;
(2)去分母得:2x=3-4x+4,
移项合并得:6x=7,
解得:x=$\frac{7}{6}$,
经检验x=$\frac{7}{6}$是分式方程的解;
(3)去分母得:4x+2=4,
解得:x=$\frac{1}{2}$,
经检验x=$\frac{1}{2}$是分式方程的解;
(4)去分母得:3x-6-x-2=0,
移项合并得:2x=8,
解得:x=4,
经检验x=4是分式方程的解;
(5)去分母得:x2-x=x2-2x-3,
解得:x=-3,
经检验x=-3是分式方程的解;
(6)去分母得:x-3+x-2=-3,
移项合并得:2x=2,
解得:x=1,
经检验x=1是分式方程的解;
(7)去分母得:12x+6=5x,
移项合并得:7x=-6,
解得:x=-$\frac{6}{7}$,
经检验x=-$\frac{6}{7}$是分式方程的解;
(8)去分母得:9x-3-2=5,
解得:x=$\frac{10}{9}$,
经检验x=$\frac{10}{9}$是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
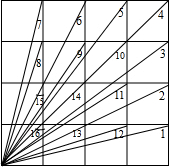 如图,是一个4×4的方格,
如图,是一个4×4的方格,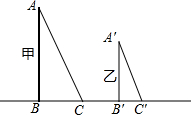 同一时刻,不同高度的物体的影子的长短不相同,物高与影长之间存在“物高A:影长A=物高B:影长B(请证明此结论)
同一时刻,不同高度的物体的影子的长短不相同,物高与影长之间存在“物高A:影长A=物高B:影长B(请证明此结论) 如图,Rt△DEF是由Rt△ABC沿BC方向平移得到的,如果AB=8,BE=4,DH=3,则△HEC的面积为$\frac{50}{3}$.
如图,Rt△DEF是由Rt△ABC沿BC方向平移得到的,如果AB=8,BE=4,DH=3,则△HEC的面积为$\frac{50}{3}$.