题目内容
11.化简($\sqrt{2-m}$)2+$\sqrt{(m-5)^{2}}$得7-2m.分析 先求出m的范围,再根据二次根式的性质进行化简即可.
解答 解:∵要使$\sqrt{2-m}$有意义,2-m≥0,
解得:m≤2,
∴($\sqrt{2-m}$)2+$\sqrt{(m-5)^{2}}$
=2-m+5-m
=7-2m,
故答案为:7-2m.
点评 本题考查了二次根式的性质和二次根式有意义的条件,二次根式的乘法等知识点,能正确根据二次根式的性质进行化简是解此题的关键.

练习册系列答案
相关题目
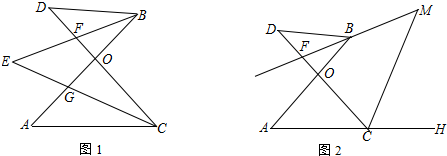
6. 如图所示,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
如图所示,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
 如图所示,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
如图所示,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )| A. | $\frac{4}{3}$π-$\sqrt{3}$ | B. | 2π-2$\sqrt{3}$ | C. | $\frac{2}{3}$π-$\sqrt{3}$ | D. | $\frac{1}{3}$π |
 如图,已知斜坡 AB 的坡度为 1:3.若坡长 AB=10m,则坡高 BC=$\sqrt{10}$m.
如图,已知斜坡 AB 的坡度为 1:3.若坡长 AB=10m,则坡高 BC=$\sqrt{10}$m. 如图,△ABC中,∠BAC=30°,将△ABC绕点A按顺时针方向旋转85°,对应得到△ADE,则∠DAE的度数为30度.
如图,△ABC中,∠BAC=30°,将△ABC绕点A按顺时针方向旋转85°,对应得到△ADE,则∠DAE的度数为30度.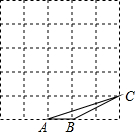 如图,在边长为1的5×5的正方形网格中有一格点△ABC,在网格中找一格点△DEF与△ABC相似,则△DEF面积的最大值为( )
如图,在边长为1的5×5的正方形网格中有一格点△ABC,在网格中找一格点△DEF与△ABC相似,则△DEF面积的最大值为( ) 如图,在地面上离旗杆BC底部18米的A处,用测角仪测得旗杆顶端C的仰角为30°,已知测角仪AD的高度为1.5米,那么旗杆BC的高度为6$\sqrt{3}$+1.5米.
如图,在地面上离旗杆BC底部18米的A处,用测角仪测得旗杆顶端C的仰角为30°,已知测角仪AD的高度为1.5米,那么旗杆BC的高度为6$\sqrt{3}$+1.5米.