Question

16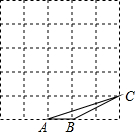．如图，在边长为1的5×5的正方形网格中有一格点△ABC，在网格中找一格点△DEF与△ABC相似，则△DEF面积的最大值为（　　）

• A． 2
• B． 2.5
• C． 3
• D． 3.5

Answer 1

分析 要让△ABC的相似三角形最大，就要让AC为网格最大的对角线，据此可根据相似三角形的性质解答．

解答 解：由勾股定理得：BC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$，△ABC的三边分别是1，$\sqrt{5}$，$\sqrt{10}$，
要让△ABC的相似三角形最大，就要让DF为网格最大的对角线，即是$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$，
所以这两个相似三角形的相似比是$\sqrt{10}$：5$\sqrt{2}$=1：$\sqrt{5}$，面积比为1：5，
△ABC的面积为$\frac{1}{2}$×1×1=$\frac{1}{2}$，
所以△DEF的最大面积是，$\frac{1}{2}$×5=2.5．
故选B．

点评 本题考查了相似三角形的判定与性质，关键是先求出最大的相似三角形，然后再利用面积比等于相似比的平方．