题目内容
14.先化简,再求值:$\frac{{m}^{2}-2m+1}{{m}^{2}-1}$÷(m-1-$\frac{m-1}{m+1}$),其中m=$\sqrt{3}$.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把m的值代入计算即可求出值.
解答 解:原式=$\frac{(m-1)^{2}}{(m+1)(m-1)}$•$\frac{m+1}{{m}^{2}-1-m+1}$=$\frac{(m-1)^{2}}{(m+1)(m-1)}$•$\frac{m+1}{m(m-1)}$=$\frac{1}{m}$,
当m=$\sqrt{3}$时,原式=$\frac{\sqrt{3}}{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.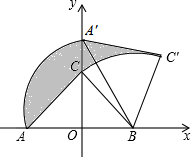 如图,Rt△ABC中,∠ACB=90°,AC=BC=2,在以AB的中点O为坐标原点、AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴正半轴上的A′处,则图中阴影部分面积为( )
如图,Rt△ABC中,∠ACB=90°,AC=BC=2,在以AB的中点O为坐标原点、AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴正半轴上的A′处,则图中阴影部分面积为( )
 如图,Rt△ABC中,∠ACB=90°,AC=BC=2,在以AB的中点O为坐标原点、AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴正半轴上的A′处,则图中阴影部分面积为( )
如图,Rt△ABC中,∠ACB=90°,AC=BC=2,在以AB的中点O为坐标原点、AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴正半轴上的A′处,则图中阴影部分面积为( )| A. | $\frac{4π}{3}$-2 | B. | $\frac{4π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{2π}{3}$-2 |
19.2015年1月份,无锡市某周的日最低气温统计如下表,则这七天中日最低气温的众数和中位数分别是( )
| 日期 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 最低气温/℃ | 2 | 4 | 5 | 3 | 4 | 6 | 7 |
| A. | 4,4 | B. | 5,4 | C. | 4,3 | D. | 4,4.5 |
3.据统计,2015年5月1日黄金周的第一天,泰山门票收益达到24万元,这个数据用科学记数法表示为( )元.
| A. | 24×104 | B. | 2.4×105 | C. | 0.24×106 | D. | 2.4×10 |
4.自从2012年9月1日昌平区首批50辆纯电动出租车正式运营以来,电动出租车以绿色环保受到市民的广泛欢迎,给市民的生活带来了很大方便.下表是行驶15公里以内普通燃油出租车和纯电动出租车的运营价格:
老张每天从家去单位打出租车上班(路程在15公里以内),结果发现正常情况下乘坐纯电动出租车比燃油出租车平均每公里节省0.8元,求老张家到单位的路程是多少公里?
| 车型 | 起步公里数 | 起步价格 | 超出起步公里数后的单价 |
| 普通燃油型 | 3 | 13元 | 2.3元/公里 |
| 纯电动型 | 3 | 8元 | 2元/公里 |
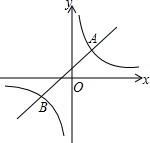 如图,在平面直角坐标系中,一次函数与反比例函数的图象相交于A(2,1)、B(-1,-2)两点.
如图,在平面直角坐标系中,一次函数与反比例函数的图象相交于A(2,1)、B(-1,-2)两点.