题目内容
 如图,直线y=-
如图,直线y=-
| ||
| 3 |
2
| ||
| 3 |
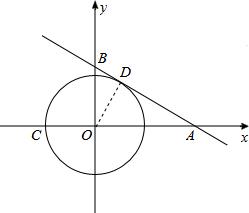
(1)求A、B、C的坐标.
(2)求过点A、B、C的二次函数的解析式.
(3)在(2)中的二次函数图象上是否存在于不同于点B的点P,使得S△PAC=S△ABC?如果存在,请求出P点的坐标;如不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)在解析式中令y=0,即可求得A的横坐标,令x=0,即可求得B的纵坐标,在直角△OAB中,令三角函数求得∠BAO的度数,然后连接OD,在直角△OAD中,利用三角函数求得OD的长,则OC即可求得,从而求得C的坐标;
(2)利用待定系数法即可求得二次函数的解析式;
(3)S△PAC=S△ABC,则P的纵坐标与B的纵坐标相等或互为相反数,以及纵坐标,代入函数的解析式即可求得横坐标.
(2)利用待定系数法即可求得二次函数的解析式;
(3)S△PAC=S△ABC,则P的纵坐标与B的纵坐标相等或互为相反数,以及纵坐标,代入函数的解析式即可求得横坐标.
解答:解:(1)在y=-
x+
中,令y=0,解得:x=2,则A的坐标是(2,0);
在y=-
x+
中,令x=0,解得y=
,则B的坐标是(0,
).
则OA=2,OB=
,
则tan∠BAO=
=
,
∠BAO=30°.
连接OD,
∵直线AB相切于点D,
∴OD⊥AB,
∴OD=OA•sin∠BAO=2×
=1,
∴OC=OD=1,
∴C的坐标是(-1,0);
(2)设二次函数的解析式是y=a(x+1)(x-2),
把(0,
)代入得:-2a=
,解得:a=-
.
则二次函数的解析式是:y=-
(x+1)(x-2);
(3)在y=-
(x+1)(x-2)中,令y=
,得:-
(x+1)(x-2)=
,
解得:x=1或0(舍去),
此时P的坐标是(1,
),
在y=-
(x+1)(x-2)中,令y=-
,得:-
(x+1)(x-2)=-
,
解得:x=
.
则P的坐标是(
,-
)或(
,-
).
则P的坐标是:(1,
)或(
,-
)或(
,-
).
| ||
| 3 |
2
| ||
| 3 |
在y=-
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |

则OA=2,OB=
2
| ||
| 3 |
则tan∠BAO=
| OB |
| OA |
| ||
| 3 |
∠BAO=30°.
连接OD,
∵直线AB相切于点D,
∴OD⊥AB,
∴OD=OA•sin∠BAO=2×
| 1 |
| 2 |
∴OC=OD=1,
∴C的坐标是(-1,0);
(2)设二次函数的解析式是y=a(x+1)(x-2),
把(0,
2
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
则二次函数的解析式是:y=-
| ||
| 3 |
(3)在y=-
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
解得:x=1或0(舍去),
此时P的坐标是(1,
2
| ||
| 3 |
在y=-
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
解得:x=
1±
| ||
| 2 |
则P的坐标是(
1+
| ||
| 2 |
2
| ||
| 3 |
1-
| ||
| 2 |
2
| ||
| 3 |
则P的坐标是:(1,
2
| ||
| 3 |
1+
| ||
| 2 |
2
| ||
| 3 |
1-
| ||
| 2 |
2
| ||
| 3 |
点评:本题考查了待定系数法求函数的解析式,以及圆的切线的性质和三角函数,正确理解P的纵坐标是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,左边的楼高AB=60m,右边的楼高CD=24m,且BC=30m,地面上的目标P位于距C点15m处.
如图,左边的楼高AB=60m,右边的楼高CD=24m,且BC=30m,地面上的目标P位于距C点15m处. 如图,在半径为4的半圆中,有一内接△ABC,其中AB为直径.
如图,在半径为4的半圆中,有一内接△ABC,其中AB为直径.