题目内容
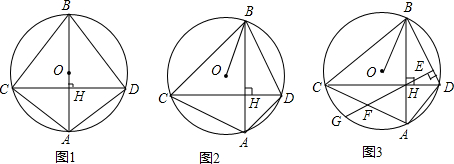
2. 一个靶子如图所示,已知中心10环的半径r=10cm,9环的半径R1=20cm,8环的半径R2=40cm,如果每发子弹都打在靶上并取得环数.
一个靶子如图所示,已知中心10环的半径r=10cm,9环的半径R1=20cm,8环的半径R2=40cm,如果每发子弹都打在靶上并取得环数.求:(1)击中10环的可能性;
(2)击中9环或10环的可能性;
(3)击中8环的可能性.
分析 (1)根据几何概率的计算方法,用10环所在的圆环面积除以最大圆的面积即可;
(2)根据几何概率的计算方法,用9环或10环所在的圆环面积除以最大圆的面积即可;
(3)根据几何概率的计算方法,用8环所在的圆环面积除以最大圆的面积即可.
解答 解:(1)射击1次击中10环的概率=$\frac{π•1{0}^{2}}{π•4{0}^{2}}=\frac{1}{16}$,
(2)击中9环或10环的可能性=$\frac{π•2{0}^{2}}{π•4{0}^{2}}=\frac{1}{4}$;
(3)击中8环的可能性=$\frac{π•4{0}^{2}-π•2{0}^{2}}{π•4{0}^{2}}=\frac{3}{4}$.
点评 本题考查了几何概率:求概率时,已知和未知与几何有关的就是几何概率.计算方法是长度比,面积比,体积比等.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
12.81的算术平方根是( )
| A. | 9 | B. | ±9 | C. | 3 | D. | ±3 |
13.下列计算正确的是( )
| A. | a3+a2=a5 | B. | a4-a2=a2 | C. | 2a-3a=-a | D. | a5•a5=2a5 |
10.有甲、乙两个不透明的袋子中装着只有颜色不同的小球,甲袋中有两个红球,乙袋中有一个红球,一个白球,从两个袋中各摸出一个球,则两个球都是红球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
11.计算b2•(-b3)2的结果是( )
| A. | b8 | B. | b11 | C. | -b8 | D. | -b11 |