题目内容
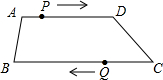 如图,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向点D以3cm/s的速度运动,到点D即停止,点Q自点C向点B以2cm/s的速度运动,到点B即停止,直线PQ截这个四边形为两个四边形,问:当P,Q同时出发,几秒后其中一个四边形为平行四边形?
如图,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向点D以3cm/s的速度运动,到点D即停止,点Q自点C向点B以2cm/s的速度运动,到点B即停止,直线PQ截这个四边形为两个四边形,问:当P,Q同时出发,几秒后其中一个四边形为平行四边形?考点:平行四边形的判定
专题:动点型
分析:设当P,Q同时出发,t秒后其中一个四边形为平行四边形,则AP=3tcm,DP=(24-3t)cm,CQ=2tcm,BQ=(30-2t)cm,分为两种情况:①当ABQP是平行四边形时,根据AP=BQ得出方程,求出方程的解即可;②当CDPQ是平行四边形时,根据DP=CQ得出方程,求出方程的解即可.
解答:解:设当P,Q同时出发,t秒后其中一个四边形为平行四边形,
则AP=3tcm,DP=(24-3t)cm,CQ=2tcm,BQ=(30-2t)cm,
①当ABQP是平行四边形时,
AP=BQ,
即3t=30-2t,
解得:t=6;
②当CDPQ是平行四边形时,
DP=CQ,
即24-3t=2t,
解得:t=4.8;
即当当P,Q同时出发,6秒或4.8秒后其中一个四边形为平行四边形.
则AP=3tcm,DP=(24-3t)cm,CQ=2tcm,BQ=(30-2t)cm,
①当ABQP是平行四边形时,
AP=BQ,
即3t=30-2t,
解得:t=6;
②当CDPQ是平行四边形时,
DP=CQ,
即24-3t=2t,
解得:t=4.8;
即当当P,Q同时出发,6秒或4.8秒后其中一个四边形为平行四边形.
点评:本题考查了平行四边形的性质的应用,能正确运用平行四边形的性质得出方程是解此题的关键,用了分类思想和方程思想,难度适中.

练习册系列答案
相关题目
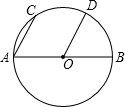 如图,AB是⊙O的直径,OD∥AC,
如图,AB是⊙O的直径,OD∥AC,
 如图,AD是直角三角形△ABC斜边上的高
如图,AD是直角三角形△ABC斜边上的高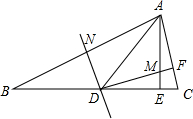 如图,在△ABC中,AE⊥BC于点E,∠B=22.5°,AB的垂直平分线DN交BC于点D,交AB于点N,DF⊥AC于点F,交AE于点M,求证:EM=EC.
如图,在△ABC中,AE⊥BC于点E,∠B=22.5°,AB的垂直平分线DN交BC于点D,交AB于点N,DF⊥AC于点F,交AE于点M,求证:EM=EC.
 如图,在△ABC中,∠C=90°,D是AC的中点,DE⊥AB于点E.求证:BC2=BE2-AE2.
如图,在△ABC中,∠C=90°,D是AC的中点,DE⊥AB于点E.求证:BC2=BE2-AE2.