题目内容
如图，在△ABC中，∠C=90°，D是AC的中点，DE⊥AB于点E．求证：BC2=BE2-AE2．考点：勾股定理
专题：证明题
分析：连接BD，根据勾股定理可知BE2-AE2=（BD2-DE2）-（AD2-DE2）=BD2-AD2=（BC2+CD2）-AD2=BC2，故可得出结论．
解答：
证明：连接BD，
∵D是AC的中点，
∴CD=AD．
∵∠C=90°，DE⊥AB，
∴BE2-AE2=（BD2-DE2）-（AD2-DE2）=BD2-AD2=（BC2+CD2）-AD2=BC2．
证明：连接BD，∵D是AC的中点，
∴CD=AD．
∵∠C=90°，DE⊥AB，
∴BE2-AE2=（BD2-DE2）-（AD2-DE2）=BD2-AD2=（BC2+CD2）-AD2=BC2．
点评：本题考查的是勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
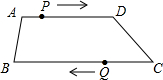如图，在四边形ABCD中，AD∥BC，AD=24cm，BC=30cm，点P自点A向点D以3cm/s的速度运动，到点D即停止，点Q自点C向点B以2cm/s的速度运动，到点B即停止，直线PQ截这个四边形为两个四边形，问：当P，Q同时出发，几秒后其中一个四边形为平行四边形？
如图，从电线杆离地面15m的A点处向地面拉一条长17m的钢索电线杆，这条钢索在地面的固定点B距离电线杆底部C点有多远？
在△ABC中，AB=AC=25，BC=40，AD为△ABC中BC边上的中线，求AD的长．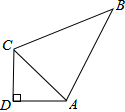
如图，四边形ABCD中，AB=13，BC=12，CD=3，AD=4，若∠D=90°，求△ABC的面积．
如图，?ABCD的对角线AC、BD相交于点O，△AOB是等边三角形，AB=5m．求这个平行四边形的面积．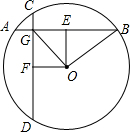
如图，在⊙O中，弦AB=CD，AB⊥CD，垂足为G，OE⊥AB，OF⊥CD，垂足分别为E，F，连接OG，OB．
已知：如图，AD∥CB，AD=CB，求证：△ABC≌△CDA．