题目内容
10.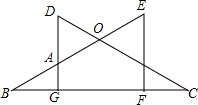 如图,已知CD=BE,DG⊥BC于点G,EF⊥BC于点F,且DG=EF.
如图,已知CD=BE,DG⊥BC于点G,EF⊥BC于点F,且DG=EF.(1)求证:△DGC≌△EFB;
(2)OB=OC吗?请说明理由;
(3)若∠B=30°,△ADO是什么三角形?
分析 (1)根据直角边和斜边对应相等的两直角三角形全等,可得答案;
(2)根据全等三角形的性质,可得∠B与∠C的关系,根据等腰三角形的判定,可得答案;
(3)根据直角三角形的性质,可得∠D,∠BAG的度数,根据对顶角的性质,可得∠DAO的度数,根据等边三角形的判定,可得答案.
解答 (1)证明:∵DG⊥BC,EF⊥BG
∴∠DGC=∠EFB=90°.
在Rt△DGC和Rt△EFB中,
$\left\{\begin{array}{l}{CD=BE}\\{DG=EF}\end{array}\right.$
∴Rt△DGC≌Rt△EFB(HL).
(2)答:OB=OC,理由:
证明:∵Rt△DGC≌Rt△EFB,
∴∠B=∠C
∴OB=OC;
(3)解:∵∠B=∠C=30°,
∴∠BAG=90°-∠B=60°,∠D=90°-∠C=60°.
由对顶角相等,得
∠DAO=∠BAG=60°.
∴∠DAO=∠D=60°,
△ADO是等边三角形..
点评 本题考查了全等三角形的判定与性质,利用了全等三角形的判定与性质,等腰三角形的判定,等边三角形的判定.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
20.一个角的余角是30度,则这个角的补角是( )
| A. | 45度 | B. | 60度 | C. | 90度 | D. | 120度 |
1.下列运算结果正确的是( )
| A. | a3•a4=a12 | B. | a2+a2=a4 | C. | (-a2)3=-a6 | D. | (3a)3=3a3 |
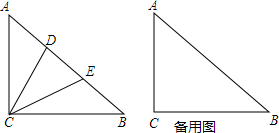
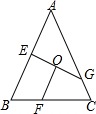 如图,在△ABC中,AB=AC,点E、F、G分别在边AB、BC、AC上,CG=BF,BE=CF,O是EG的中点,求证:FO⊥GE.
如图,在△ABC中,AB=AC,点E、F、G分别在边AB、BC、AC上,CG=BF,BE=CF,O是EG的中点,求证:FO⊥GE.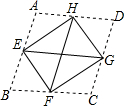 如图,将菱形ABCD的四个角沿相邻两边中点的连线向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,已知EH=8cm,EF=6cm.
如图,将菱形ABCD的四个角沿相邻两边中点的连线向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,已知EH=8cm,EF=6cm.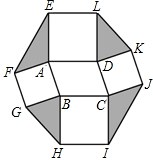 如图,以?ABCD的四条边为边,分别向外作正方形,连结EF,GH,IJ,KL.如果?ABCD的面积为8,则图中阴影部分四个三角形的面积和为( )
如图,以?ABCD的四条边为边,分别向外作正方形,连结EF,GH,IJ,KL.如果?ABCD的面积为8,则图中阴影部分四个三角形的面积和为( ) 如图,O是直线AB上一点,OD平分∠BOC,若∠α=25°,则∠AOC=130°.
如图,O是直线AB上一点,OD平分∠BOC,若∠α=25°,则∠AOC=130°.