题目内容
16.已知,BC∥OA,∠B=∠A=108°,试解答下列问题:
(1)如图①,则∠O=72°,则OB与AC的位置关系为平行
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于36°;
(3)在第(2)题的条件下,若平行移动AC到如图③所示位置.
①在AC移动的过程中,∠OCB与∠OFB的比值是否发生改变,若不改变求出其比值,若要改变说明理由;
②当∠OEB=∠OCA时,求∠OCA.
分析 (1)根据平行线的性质得出∠B+∠O=180°,求出∠O=72°,求出∠O+∠A=180°,根据平行线的判定得出即可;
(2)根据角平分线定义求出∠EOC=$\frac{1}{2}∠BOA$=36°,即可得出答案;
(3)①不变,求出∠OFB=2∠OCB,即可得出答案;
②设∠BOE=∠EOF=α,∠FOC=∠COA=β,求出∠OCA=∠BOC=2α+β,α=β=18°,即可得出答案.
解答 解:(1)∵BC∥OA,
∴∠B+∠O=180°,
∵∠B=108°,
∴∠O=72°,
∵∠A=108°,
∴∠O+∠A=180°,
∴OB∥AC,
故答案为:72°,平行;
(2)∵∠FOC=∠AOC,OE平分∠BOF,∠BOA=72°,
∴∠EOC=∠EOF+∠FOC=$\frac{1}{2}$∠BOF+$\frac{1}{2}$∠FOA=$\frac{1}{2}∠BOA$=36°,
故答案为:36°;
(3)①不变,
∵BC∥OA,
∴∠OCB=∠AOC,
又∵∠FOC=∠AOC,
∴∠FOC=∠OCB,
又∵BC∥OA,
∴∠OFB=∠FOA=2∠FOC,
∴∠OFB=2∠OCB,
即∠OCB:∠OFB=1:2.
即∠OCB与∠OFB的比值为$\frac{1}{2}$;
②由(1)知:OB∥AC,
∴∠OCA=∠BOC,
由(2)可以设:∠BOE=∠EOF=α,∠FOC=∠COA=β,
∴∠OCA=∠BOC=2α+β
由(1)知:BC∥OA,
∴∠OEB=∠EOA=α+β+β=α+2β
∵∠OEB=∠OCA
∴2α+β=α+2β
∴α=β
∵∠AOB=72°,
∴α=β=18°
∴∠OCA=2α+β=36°+18°=54°.
点评 本题考查了平行线的性质和判定,能灵活运用平行线的性质和判定进行推理是解此题的关键.

练习册系列答案
相关题目
4.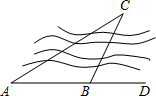 如图,要测量凉亭C到河岸AD的距离,在河岸相距200米的A,B两点,分别测得∠CAB=30°,∠CBD=60°,则凉亭C到河岸AD的距离为( )
如图,要测量凉亭C到河岸AD的距离,在河岸相距200米的A,B两点,分别测得∠CAB=30°,∠CBD=60°,则凉亭C到河岸AD的距离为( )
 如图,要测量凉亭C到河岸AD的距离,在河岸相距200米的A,B两点,分别测得∠CAB=30°,∠CBD=60°,则凉亭C到河岸AD的距离为( )
如图,要测量凉亭C到河岸AD的距离,在河岸相距200米的A,B两点,分别测得∠CAB=30°,∠CBD=60°,则凉亭C到河岸AD的距离为( )| A. | 100米 | B. | 100$\sqrt{3}$米 | C. | 200米 | D. | 200$\sqrt{3}$米 |
5.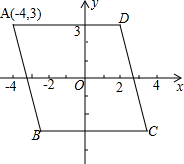 如图,菱形ABCD的中心是坐标原点,且AD∥x轴,点A的坐标为(-4,3),那么C点的坐标为( )
如图,菱形ABCD的中心是坐标原点,且AD∥x轴,点A的坐标为(-4,3),那么C点的坐标为( )
 如图,菱形ABCD的中心是坐标原点,且AD∥x轴,点A的坐标为(-4,3),那么C点的坐标为( )
如图,菱形ABCD的中心是坐标原点,且AD∥x轴,点A的坐标为(-4,3),那么C点的坐标为( )| A. | (4,-3) | B. | (3,-4) | C. | (4,-4) | D. | (3,-3) |
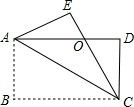 如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.
如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.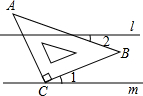 如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的和是多少度?并证明你的结论.
如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的和是多少度?并证明你的结论. 如图:AC∥ED,∠A=∠EDF,试说明AB∥FD.
如图:AC∥ED,∠A=∠EDF,试说明AB∥FD.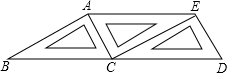 如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有( )
如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有( )