题目内容
1.如图,顺次次连接正三角形、正四边形、正五边形、正六边形的各边中点,分别得到△PQR,四边形PQRH,五边形PQRHS,六边形PQRHST,小明发现,它们都是正多边形,请你选择其一,给出证明.
分析 利用全等三角形的性质,根据正多边形的定义一一证明即可.
解答 解:①如图1中,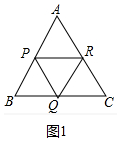
∵△ABC是等边三角形,
∴AB=CB=AC,
∵PA=PB,AR=RC,BQ=CQ,
∴PR=$\frac{1}{2}$BC,PQ=$\frac{1}{2}$AC,RQ=$\frac{1}{2}$AB,
∴PR=PQ=RQ,
∴△PQR是等边三角形.
②如图2中,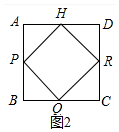
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°,
∵PA=PB,QB=QC,RD=RC,AH=HD,
∴AP=PB=BQ=CQ=CR=DR=DH=AH,
∴△APH≌△BQP≌△CRQ≌△DRH,
∴PH=PQ=RQ=HR,
∴四边形PQRH是菱形,
∵∠AHP=∠DHR=45°,
∴∠PHR=90°,
∴四边形PQRH是正方形.
③如图3中,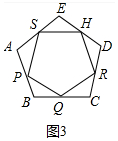
同理可证△APD≌△BQP≌△CRQ≌△DHR≌△ESH≌△APS,
∴PS=PQ=RQ=HR=SH,
∵∠ASP=∠APS=∠ESH=∠EHS=∠BPQ=∠BQP,
∴∠HSP=∠SPQ,同理可证∠PSH=∠SHR=∠HRQ=∠RQP,
∴五边形PSHRQ是正五边形.
④如图4中,同理可证△FTS≌△APT≌△BQP≌△CRQ≌△DHR≌△ESH,∠STP=∠TPQ=∠PQR=∠QRH=∠RHS=∠HST,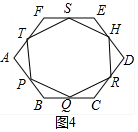
∴TP=PQ=QR=RH=HS=ST,
∴六边形PQRHST是正六边形.
点评 本题考查正多边形和圆、三角形中位线定理、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
9.下列等式从左到右的变形是因式分解的是( )
| A. | 6x2y2=xy•6xy | B. | 2x2-8x-5=2x(x-4)-5 | ||
| C. | x2+3x-4=(x-1)(x+4) | D. | x2+1=x(x+$\frac{1}{x}$) |
6.用配方法解方程x2-2x-4=0时,配方后所得的方程为( )
| A. | (x-1)2=0 | B. | (x-1)2=5 | C. | (x+1)2=0 | D. | (x+1)2=5 |
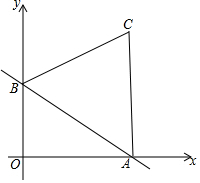 如图.直线y=-$\frac{\sqrt{3}}{3}$x+1和x、y轴分别交于点A、B,∠BAO=30°,以线段AB为边在第一象限内作等边三角形ABC.如果在第一象限内有一点P(m,1),且△ABP的面积与△ABC的面积相等,求m的值.
如图.直线y=-$\frac{\sqrt{3}}{3}$x+1和x、y轴分别交于点A、B,∠BAO=30°,以线段AB为边在第一象限内作等边三角形ABC.如果在第一象限内有一点P(m,1),且△ABP的面积与△ABC的面积相等,求m的值.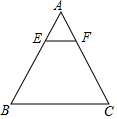 如图,在△ABC中,EF∥BC,$\frac{AE}{EB}$=$\frac{1}{2}$,EF=3,则BC的值为9.
如图,在△ABC中,EF∥BC,$\frac{AE}{EB}$=$\frac{1}{2}$,EF=3,则BC的值为9.