题目内容
13.商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施,经调查发现,每件商品每降价1元,商场平均每天可多售出2件,据此规律,请回答:(1)设每件商品降价x元,则商场此商品可多售出2x件,此商品每件盈利(50-x)元,此商品每天可销售(30+2x)件.
(2)每件商品降价多少元时,商场日盈利可达到2100元?
分析 (1)降价1元,可多售出2件,降价x元,可多售出2x件,盈利的钱数=原来的盈利-降低的钱数;
(2)等量关系为:每件商品的盈利×可卖出商品的件数=2100,把相关数值代入计算得到合适的解即可.
解答 解:(1)设每件商品降价x元,则商场此商品可多售出 2x件,此商品每件盈利 (50-x)元,此商品每天可销售 (30+2x)件.
故答案是:2x,(50-x),(30+2x);
(2)解:设每件商品降价x元,由题意得:
(50-x)(30+2x)=2100,
化简得:x2-35x+300=0,
解得:x1=15,x2=20,
∵该商场为了尽快减少库存,则x=15不合题意,舍去.
∴x=20.
答:每件商品降价20元,商场日盈利可达2100元.
点评 此题主要考查了一元二次方程的应用;得到可卖出商品数量是解决本题的易错点;得到总盈利2100的等量关系是解决本题的关键.

练习册系列答案
相关题目
20.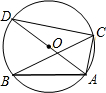 如图,△ABC内接于圆O,AD是圆O的直径,∠ABC=30°,则∠CAD的度数等于( )
如图,△ABC内接于圆O,AD是圆O的直径,∠ABC=30°,则∠CAD的度数等于( )
 如图,△ABC内接于圆O,AD是圆O的直径,∠ABC=30°,则∠CAD的度数等于( )
如图,△ABC内接于圆O,AD是圆O的直径,∠ABC=30°,则∠CAD的度数等于( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
 已知点P(x,y),现将它向左平移5个单位,再向下平移4个单位,得到点P′(-2y,-2x).
已知点P(x,y),现将它向左平移5个单位,再向下平移4个单位,得到点P′(-2y,-2x).