题目内容
10．
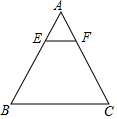如图，在△ABC中，EF∥BC，$\frac{AE}{EB}$=$\frac{1}{2}$，EF=3，则BC的值为9．
分析 由EF∥BC，可得△AEF∽△ABC，所以AE：AB=EF：BC，把已知线段之间的数量关系和长度代入比例式即可求出BC的长．
解答 解：∵EF∥BC，
∴△AEF∽△ABC，
∴AE：AB=EF：BC，
∵$\frac{AE}{EB}$=$\frac{1}{2}$，
∴AE：AB=1：3，
∵EF=3，
∴1：3=3：BC，
∴BC=9，
答：BC的长是9，
故答案为：9．
点评 本题考查了相似三角形的判定和性质，题目比较简单，熟记相似三角形的各种性质是解题关键．
练习册系列答案
相关题目
20．
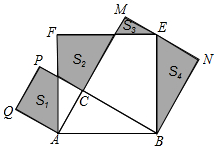如图，Rt△ABC中，∠C=90°，AC=3，BC=4．分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN，四块阴影部分的面积分别为S1、S2、S3、S4．则S1-S2+S3+S4等于（ ）
如图，Rt△ABC中，∠C=90°，AC=3，BC=4．分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN，四块阴影部分的面积分别为S1、S2、S3、S4．则S1-S2+S3+S4等于（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 12 |
15．由四舍五入法取近似数：23.96精确到十分位是（ ）
| A． | 24.0 | B． | 24 | C． | 24.00 | D． | 23.9 |