题目内容
6.某商场将进货单价为40元的裤子按50元每件出售时,每月能卖出500件.已知该商场裤子每涨价1元.其月销售量就将减少10件.若这种裤子的售价为x元/件,该裤子每月获得的利润为y元.(1)求出y与x之间的函数关系式;
(2)商场将售价定为多少时.获得的月利润最大?最大的月利涧是多少?
分析 (1)根据题意利用销量×每件利润=总利润,进而得出即可;
(2)设最大利润为y元,根据(1)列出y与x的二次函数关系式,转化为顶点式可得最值.
解答 解:(1)根据题意可得:
y=(x-40)[500-10(x-50)]
=-10x2+1400x+40000;
(2)y=-10x2+1400x+40000
=-10(x-60)2+9000,
当x=60时,ymax=9000,
答:商场将售价定为60元时.获得的月利润最大,最大的月利润是9000元.
点评 本题考查一元二次方程的应用以及运用二次函数与一元二次方程的关系解决最值问题,得到每件商品获得的利润和卖出商品件数是解决本题的突破点,构建二次函数模型是解决最大利润问题的关键.

练习册系列答案
相关题目
16. 如图,在数轴上有a,b两个实数,则化简|b-a|+|a+b|的结果是( )
如图,在数轴上有a,b两个实数,则化简|b-a|+|a+b|的结果是( )
 如图,在数轴上有a,b两个实数,则化简|b-a|+|a+b|的结果是( )
如图,在数轴上有a,b两个实数,则化简|b-a|+|a+b|的结果是( )| A. | -2b | B. | 2a | C. | 2b | D. | 0 |
17.若a的倒数是它本身,b的平方根等于它本身,那么(a2+b)2的值是( )
| A. | 1 | B. | 8 | C. | ±1 | D. | ±8 |
14.新泰市2014级四年制学生人数约为1.33万名,从中抽取300名学生的八年级上学期其中考试数学成绩进行分析,在本次调查中,样本指的是( )
| A. | 300名考生的数学成绩 | B. | 300 | ||
| C. | 1.33万名考生的数学成绩 | D. | 300名考生 |
 如图,两个反比例函数y1=$\frac{{k}_{1}}{x}$(其中k1>0)和y2=$\frac{3}{x}$在第一象限内的图象依次是C1和C2,点P在C1上,矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为$\sqrt{3}$.
如图,两个反比例函数y1=$\frac{{k}_{1}}{x}$(其中k1>0)和y2=$\frac{3}{x}$在第一象限内的图象依次是C1和C2,点P在C1上,矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为$\sqrt{3}$. 如图,已知?ABCD中,对角线AC与BD交于点O,∠ABD=2∠DBC,AE⊥BD于E.
如图,已知?ABCD中,对角线AC与BD交于点O,∠ABD=2∠DBC,AE⊥BD于E.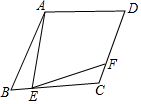 如图,四边形ABCD是菱形.∠ABC=60°,点E是BC边上一点,∠AEF=60°,且EF交直线CD于点F,求证:AE=EF.
如图,四边形ABCD是菱形.∠ABC=60°,点E是BC边上一点,∠AEF=60°,且EF交直线CD于点F,求证:AE=EF.