题目内容
4.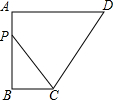 如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.若P是四边形边上一动点,且∠BPC=30°,则CP的长为4或2或2$\sqrt{3}$.
如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.若P是四边形边上一动点,且∠BPC=30°,则CP的长为4或2或2$\sqrt{3}$.
分析 在Rt△PBC中,根据含30度角的直角三角形的性质,可得CP=2BC=4,据此解答即可.
解答 解:∵AB⊥BC,
∴∠PBC=90°,
在Rt△PBC中,
∵∠BPC=30°,
∴CP=2BC=2×2=4,
即CP的长为4.
另外还有P2 ,P3下面两种情况也符合条件,此时CP2=2$\sqrt{3}$(P2C⊥BC时),CP3=2(P3C=BC时)
点评 此题主要考查了含30度角的直角三角形的性质,要熟练掌握,解答此题的关键是要明确:在直角三角形中,30°角所对的直角边等于斜边的一半.

练习册系列答案
相关题目
19.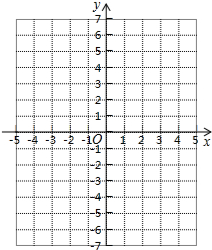 已知动点(x,y)的横纵坐标满足方程2y-x=2.
已知动点(x,y)的横纵坐标满足方程2y-x=2.
(1)请在表格中求出相应的x(或y)的值,并在图中平面直角坐标系中描出这些点:
(2)若将这五个点先向右平移5个单位长度,再向上平移3个单位长度,得到点A1,B1,C1,D1,E1,并分别写出它们的坐标.
 已知动点(x,y)的横纵坐标满足方程2y-x=2.
已知动点(x,y)的横纵坐标满足方程2y-x=2.(1)请在表格中求出相应的x(或y)的值,并在图中平面直角坐标系中描出这些点:
| 点的名称 | A | B | C | D | E |
| 点的横坐标x | -2 | 2 | |||
| 点的纵坐标y | -1 | 1 | 3 |
14.下列运算正确的是( )
| A. | a8÷a2=a4 | B. | a3+a3=a6 | C. | (a3)3=a6 | D. | (-a)2•(-a)3=-a5 |
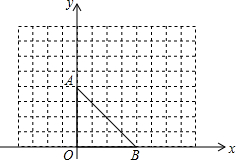 如图,点A的坐标是(0,4),点B的坐标是(4,0).
如图,点A的坐标是(0,4),点B的坐标是(4,0).