题目内容
在平面直角坐标系中,直线y=
x+3与x轴,y轴分别交于A、B两点,⊙F与x轴、y轴和直线AB分别相切于点D,E,C,求⊙F的半径.
| 3 |
| 4 |
考点:圆的综合题
专题:分类讨论
分析:由条件易求出OA、OB、AB的长及△AOB的面积,由于满足条件的圆心F的位置并不唯一,因此需分情况讨论(如图1、图2、图3、图4),连接FA、FB、FO、FD、FE、FC,然后只需利用S△OAB与S△OAF、S△OBF、S△ABF之间的等量关系就可求出⊙F的半径.
解答:解:∵直线y=
x+3与x轴、y轴分别交于A、B两点,
∴点A的坐标为(-4,0),点B的坐标为(0,3),
∴OA=4,OB=3.
∵∠AOB=90°,
∴S△AOB=
OA•OB=6,AB=
=5.
①若点F在如图1的位置,设⊙F的半径为r,
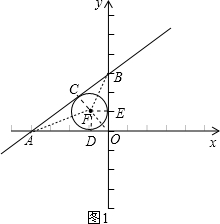
连接FA、FB、FO、FD、FE、FC,则FD=FE=FC=r.
∵⊙F与x轴、y轴和直线AB分别相切于点D、E、C,
∴FD⊥OA,FE⊥OB,FC⊥AB.
∵S△OAB=S△OAF+S△OBF+S△ABF,
∴6=
OA•FD+
OB•FE+
AB•FC,
∴6=
r(OA+OB+AB)=
r×(4+3+5),
∴r=1.
②若点F在如图2的位置,设⊙F的半径为r,
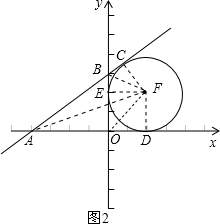
连接FA、FB、FO、FD、FE、FC,则FD=FE=FC=r.
∵⊙F与x轴、y轴和直线AB分别相切于点D、E、C,
∴FD⊥OA,FE⊥OB,FC⊥AB.
∵S△OAB=S△OAF+S△ABF-S△OBF,
∴6=
OA•FD+
AB•FC-
OB•FE,
∴6=
r(OA+AB-OB)=
r×(4+5-3),
∴r=2.
③若点F在如图3的位置,设⊙F的半径为r,
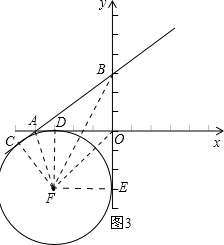
连接FA、FB、FO、FD、FE、FC,则FD=FE=FC=r.
∵⊙F与x轴、y轴和直线AB分别相切于点D、E、C,
∴FD⊥OA,FE⊥OB,FC⊥AB.
∵S△OAB=S△OBF+S△ABF-S△OAF,
∴6=
OB•FE+
AB•FC-
OA•FD,
∴6=
r(OB+AB-OA)=
r×(3+5-4),
∴r=3.
④若点F在如图4的位置,设⊙F的半径为r,
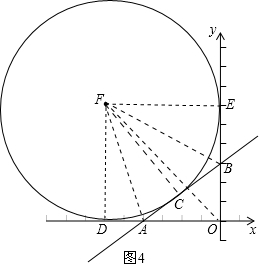
连接FA、FB、FO、FD、FE、FC,则FD=FE=FC=r.
∵⊙F与x轴、y轴和直线AB分别相切于点D、E、C,
∴FD⊥OA,FE⊥OB,FC⊥AB.
∵S△OAB=S△OAF+S△OBF-S△ABF,
∴6=
OA•FD+
OB•FE-
AB•FC,
∴6=
r(OA+OB-AB)=
r×(4+3-5),
∴r=6.
综上所述:满足条件的⊙F的半径为1或2或3或6.
| 3 |
| 4 |
∴点A的坐标为(-4,0),点B的坐标为(0,3),
∴OA=4,OB=3.
∵∠AOB=90°,
∴S△AOB=
| 1 |
| 2 |
| OA2+OB2 |
①若点F在如图1的位置,设⊙F的半径为r,

连接FA、FB、FO、FD、FE、FC,则FD=FE=FC=r.
∵⊙F与x轴、y轴和直线AB分别相切于点D、E、C,
∴FD⊥OA,FE⊥OB,FC⊥AB.
∵S△OAB=S△OAF+S△OBF+S△ABF,
∴6=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴6=
| 1 |
| 2 |
| 1 |
| 2 |
∴r=1.
②若点F在如图2的位置,设⊙F的半径为r,

连接FA、FB、FO、FD、FE、FC,则FD=FE=FC=r.
∵⊙F与x轴、y轴和直线AB分别相切于点D、E、C,
∴FD⊥OA,FE⊥OB,FC⊥AB.
∵S△OAB=S△OAF+S△ABF-S△OBF,
∴6=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴6=
| 1 |
| 2 |
| 1 |
| 2 |
∴r=2.
③若点F在如图3的位置,设⊙F的半径为r,

连接FA、FB、FO、FD、FE、FC,则FD=FE=FC=r.
∵⊙F与x轴、y轴和直线AB分别相切于点D、E、C,
∴FD⊥OA,FE⊥OB,FC⊥AB.
∵S△OAB=S△OBF+S△ABF-S△OAF,
∴6=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴6=
| 1 |
| 2 |
| 1 |
| 2 |
∴r=3.
④若点F在如图4的位置,设⊙F的半径为r,

连接FA、FB、FO、FD、FE、FC,则FD=FE=FC=r.
∵⊙F与x轴、y轴和直线AB分别相切于点D、E、C,
∴FD⊥OA,FE⊥OB,FC⊥AB.
∵S△OAB=S△OAF+S△OBF-S△ABF,
∴6=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴6=
| 1 |
| 2 |
| 1 |
| 2 |
∴r=6.
综上所述:满足条件的⊙F的半径为1或2或3或6.
点评:本题主要考查了切线的性质、直线上点的坐标特征、三角形的面积公式等知识,用到了分类讨论的数学思想,而运用面积法是解决本题的关键.

练习册系列答案
相关题目
下列各组代数式,是同类项的是( )
| A、x2与52 |
| B、-4yx与3xyπ |
| C、9ab与-3xy |
| D、-2cab与3bc |
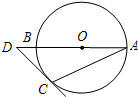 如图,AB是⊙0的直径,点D在AB的延长线上,过点D作⊙0的切线,切点为C,若∠A=25°,则∠D=( )
如图,AB是⊙0的直径,点D在AB的延长线上,过点D作⊙0的切线,切点为C,若∠A=25°,则∠D=( )| A、60° | B、65° |
| C、50° | D、40° |
若方程(t+2)x2-(t2-4)x+t=0的两个根互为相反数,则t等于( )
| A、-2 | B、2 | C、±2 | D、4 |
 一个不等式组的解在数轴上表示如图,则这个不等式组的解是
一个不等式组的解在数轴上表示如图,则这个不等式组的解是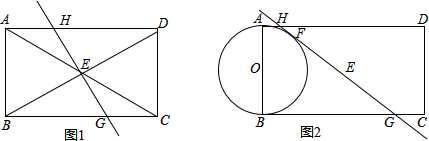
 如图,PA、PB分别切⊙O于点A、B,若∠P=70°,点C为⊙O上任一动点,则∠C的大小为
如图,PA、PB分别切⊙O于点A、B,若∠P=70°,点C为⊙O上任一动点,则∠C的大小为 如图,在Rt△ABC中,∠C=90°,CD⊥AB,如果∠A=40°,则∠1=
如图,在Rt△ABC中,∠C=90°,CD⊥AB,如果∠A=40°,则∠1=