题目内容
定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“凤凰”方程.已知方程a1x2+b1x+c1=0(a≠0)是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
| A、a1=b1 |
| B、a1=c1 |
| C、b1=c1 |
| D、a1=b1=c1 |
考点:根的判别式
专题:新定义
分析:由条件可知a1+b1+c1=0,再根据方程根的判别式得到到b12-4a1c1=0,整理可得出结论.
解答:解:
由条件可知a1+b1+c1=0,
所以b1=a1+c1,
又因为方程有两个相等的实数根,
所以△=0,即b12-4a1c1=0,
所以(a1+c1)2-4a1c1=0,
整理可得(a1-c1)2=0,
所以a1=c1,
故选B.
由条件可知a1+b1+c1=0,
所以b1=a1+c1,
又因为方程有两个相等的实数根,
所以△=0,即b12-4a1c1=0,
所以(a1+c1)2-4a1c1=0,
整理可得(a1-c1)2=0,
所以a1=c1,
故选B.
点评:本题主要考查一元二次方程判别式与根的情况的判定,由条件到到知a1+b1+c1=0和b12-4a1c1=0是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
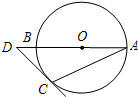 如图,AB是⊙0的直径,点D在AB的延长线上,过点D作⊙0的切线,切点为C,若∠A=25°,则∠D=( )
如图,AB是⊙0的直径,点D在AB的延长线上,过点D作⊙0的切线,切点为C,若∠A=25°,则∠D=( )| A、60° | B、65° |
| C、50° | D、40° |
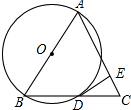 如图,在△ABC中,以AB为直径作⊙O交BC于D,DE交AC于点E.
如图,在△ABC中,以AB为直径作⊙O交BC于D,DE交AC于点E. 如图,在Rt△ABC中,∠C=90°,CD⊥AB,如果∠A=40°,则∠1=
如图,在Rt△ABC中,∠C=90°,CD⊥AB,如果∠A=40°,则∠1=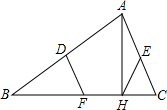 已知:如图,D、E、F分别是△ABC三边中点,AH⊥BC于H,求证:DF=EH.
已知:如图,D、E、F分别是△ABC三边中点,AH⊥BC于H,求证:DF=EH.