题目内容
19.已知|a-c-2|+(a-9b)2+(3b+3c-4)4=0,求a2016b2015c2017-a的值.分析 根据绝对值,偶次方的非负性得出a-c-2=0,a-9b=0,3b+3c-4=0,组成方程组,求出方程组的解,最后代入求出即可.
解答 解:∵|a-c-2|+(a-9b)2+(3b+3c-4)4=0,
∴a-c-2=0,a-9b=0,3b+3c-4=0,
即$\left\{\begin{array}{l}{a-c=2}\\{a-9b=0}\\{3b+3c=4}\end{array}\right.$,
解得:a=3,b=$\frac{1}{3}$,c=1,
∴a2016b2015c2017-a
=32016×($\frac{1}{3}$)2015×12017-3
=0.
点评 本题考查了偶次方、绝对值的非负性,解三元一次方程组,求代数式的值的应用,能得出关于a、b、c的方程组是解此题的关键.

练习册系列答案
相关题目
11.某保险公司推出如下的重大疾病险,根据病人的情况报销一定比例的医疗费.医疗费的报销比例标准如下表:
(1)某人在医院实际医疗费为8000元.请问能报销多少钱?
(2)若此人某次住院的自付医疗费为2600元(自付医疗费=实际医疗费-按标准报销的金额),则此人此次住院的实际医疗费为多少元?
| 费用范围 | 500元以下(含500元) | 超过500元且不超过10000元的部分 | 超过10000元的 部分 |
| 报销标准 | 不予报销 | 70% | 80% |
(2)若此人某次住院的自付医疗费为2600元(自付医疗费=实际医疗费-按标准报销的金额),则此人此次住院的实际医疗费为多少元?
 如图,在离旗杆30m的A处,用测角仪测得旗杆顶端D的仰角为30°,测得旗杆底部C的俯角为α,且tanα=$\frac{1}{30}$,试求:
如图,在离旗杆30m的A处,用测角仪测得旗杆顶端D的仰角为30°,测得旗杆底部C的俯角为α,且tanα=$\frac{1}{30}$,试求: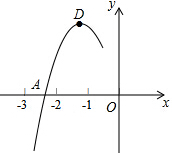 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则方程ax2+bx+c-2=0有两个相等实数根.
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则方程ax2+bx+c-2=0有两个相等实数根.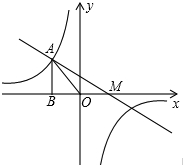 如图,点A(-2,b)是函数y=$\frac{k}{x}$的图象上的点,过点A作AB⊥x轴于点B,△AOB的面积为2,若一次函数y=ax+1的图象经过点A且与x轴交于点M,则AO:AM=$\sqrt{2}$:$\sqrt{5}$.
如图,点A(-2,b)是函数y=$\frac{k}{x}$的图象上的点,过点A作AB⊥x轴于点B,△AOB的面积为2,若一次函数y=ax+1的图象经过点A且与x轴交于点M,则AO:AM=$\sqrt{2}$:$\sqrt{5}$.