��Ŀ����
7����ͼ1��2���ڡ�ABC�У�AB=13��BC=14��BH=5��̽������ͼ1��AH��BC�ڵ�H����AH=12��AC=15����ABC�����S��ABC=84��
��չ����ͼ2����D��AC�ϣ������A��C�غϣ����ֱ����A��C��ֱ��BD�Ĵ��ߣ�����ΪE��F����BD=x��AE=m��CF=n������D���A�غ�ʱ��������ΪS��ABD=0��
��1���ú�x��m��n�Ĵ���ʽ��ʾS��ADB��S��CBD��
��2����m+n����x�ĺ�����ϵʽ������m+n�������ֵ����Сֵ��
��3���Ը�����һ��xֵ����ʱֻ��ȷ��Ψһ�ĵ�D��ֱ��д��������x��ȡֵ��Χ��

���� ̽�������ݹ��ɶ������㼴�ɣ�
��1�����������ε������ʽ���㣻
��2�����ݡ�ABC�������84���г���ϵʽ�������m+n����x�ĺ�����ϵʽ�����ͼ�������m+n�������ֵ����Сֵ��
��3�����ݵ�BD��ACʱ��m+n�����ֵ���
��� �⣺̽�����ɹ��ɶ����ã�AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=12��
AC=$\sqrt{A{H}^{2}+H{C}^{2}}$=15��
��ABC�����S��ABC=$\frac{1}{2}$��BC��AH=84��
�ʴ�Ϊ��12��15��84��
��1��S��ADB=$\frac{1}{2}$��BD��AE=$\frac{1}{2}$mx��
S��CBD=$\frac{1}{2}$��BD��CH=$\frac{1}{2}$nx��
��2��$\frac{1}{2}$mx+$\frac{1}{2}$nx=84��
m+n=$\frac{168}{x}$��
��BD��ACʱ��m+n�����ֵ15��
��BDֵ���ʱ��m+n����Сֵ��
�൱��D���C�غ�ʱm+n����Сֵ��
��m+n����СֵΪ$\frac{168}{14}$=12��
��3����BD��ACʱ��
x=BD=$\frac{168}{15}$=11.2��ֻ��ȷ��Ψһ�ĵ�D��
���� ���⿼����������ε��ۺ����ã����������ε������ʽ��������÷��������˼���ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
17������$\frac{x+2}{4}$+1=$\frac{x}{3}$��ȥ��ĸ����ȷ���ǣ�������
| A�� | 3��x+2��+12=4x | B�� | 12��x+2��+12=12x | C�� | 4��x+2��+12=3x | D�� | 3��x+2��+1=4x |
18���ڡ�ABC�У���C=90�㣬AC=3��CB=4����cotA��ֵΪ��������
| A�� | $\frac{4}{5}$ | B�� | $\frac{3}{5}$ | C�� | $\frac{4}{3}$ | D�� | $\frac{3}{4}$ |
15����ʡ��2010��7�¿�ʼʵʩ���ݵ���ƣ����������õ�۸����±���
������ij�û�2010��8�·ݵ��õ���Ϊ300�ȣ�����ɽ����Ϊ��200��0.5+��300-200����0.55=155��Ԫ����
��1����գ����С����2010��9�·ݵ��õ���Ϊ100�ȣ�����ɽ����50Ԫ��
��2�����С����2010��10�·ݵ��õ���Ϊa�ȣ�����200��a��400��������ɽ���Ѷ���Ԫ�����ú�a�Ĵ���ʽ��ʾ��������
��3�����С����2010��11��12�����¹��õ�700�ȣ�����12�·ݵ��õ����ﵽ����3����������11�·ݵ��õ���Ϊb�ȣ���С�����������¹���ɽ���Ѷ���Ԫ�����ú�b�Ĵ���ʽ��ʾ��������
| ���� | ���õ��� | ��ۣ���λ��Ԫ/�ȣ� |
| ��1�� | ���õ�����200�� | 0.5 |
| ��2�� | 200�ȣ����õ�����400�� | 0.55 |
| ��3�� | ���õ�����400�� | 0.8 |
��1����գ����С����2010��9�·ݵ��õ���Ϊ100�ȣ�����ɽ����50Ԫ��
��2�����С����2010��10�·ݵ��õ���Ϊa�ȣ�����200��a��400��������ɽ���Ѷ���Ԫ�����ú�a�Ĵ���ʽ��ʾ��������
��3�����С����2010��11��12�����¹��õ�700�ȣ�����12�·ݵ��õ����ﵽ����3����������11�·ݵ��õ���Ϊb�ȣ���С�����������¹���ɽ���Ѷ���Ԫ�����ú�b�Ĵ���ʽ��ʾ��������

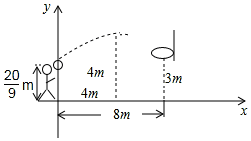 С������Ͷ���������ʱ�����$\frac{20}{9}$m������ֺ��ڿ�����������·���˶������ھ���ֵ�ˮƽ����4m���ﵽ���4m����֪�������ľ����3m���������ʱ��ˮƽ����Ϊ8m��������ͼ��ʾ��ƽ��ֱ������ϵ��
С������Ͷ���������ʱ�����$\frac{20}{9}$m������ֺ��ڿ�����������·���˶������ھ���ֵ�ˮƽ����4m���ﵽ���4m����֪�������ľ����3m���������ʱ��ˮƽ����Ϊ8m��������ͼ��ʾ��ƽ��ֱ������ϵ��