题目内容
15.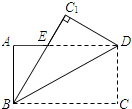 把矩形ABCD沿对角线BD对折,点C落在C1处,BC1交AD于E,AB=6cm,BC=8cm,则AE的长是$\frac{7}{4}$cm.
把矩形ABCD沿对角线BD对折,点C落在C1处,BC1交AD于E,AB=6cm,BC=8cm,则AE的长是$\frac{7}{4}$cm.
分析 由矩形的性质和折叠的性质得出∠EDB=∠DBE,证出BE=DE,设AE=xcm,则BE=DE=(8-x)cm,在Rt△ABE中,根据勾股定理得出方程,解方程即可.
解答 解:∵四边形ABCD是矩形,
∴AD=BC=8cm,∠A=90°,AD∥BC,
∴∠EDB=∠DBC,
由折叠的性质得:∠DBE=∠DBC,
∴∠EDB=∠DBE,
∴BE=DE,
设AE=xcm,
则BE=DE=(8-x)cm,
在Rt△ABE中,根据勾股定理得:AE2+AB2=BE2,
即x2+62=(8-x)2,
解得:x=$\frac{7}{4}$,
∴AE=$\frac{7}{4}$cm;
故答案为:$\frac{7}{4}$cm.
点评 本题考查了矩形的性质、翻折变换的性质、勾股定理;熟练掌握翻折变换和矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
5.利用配方法将x2-2x+3=0化为a(x-h)2+k=0 (a≠0)的形式为 ( )
| A. | (x-1)2-2=0 | B. | (x-1)2+2=0 | C. | (x+1)2+2=0 | D. | (x+1)2-2=0 |
3.函数y=$\frac{\sqrt{x}}{x-1}$中,自变量的取值范围是( )
| A. | x≥0 | B. | x≠1 | C. | x>1 | D. | x≥0,且x≠1 |
10.一组数据x1,x2,x3,…,xn的平均数是a,方差是b,那么数据2x1,2x2,2x3…2xn的平均数和方差分别是( )
| A. | 2a和2b | B. | 2a和4b | C. | 4a和2b | D. | 4a和4b |
4.下列调查中,适宜采用普查的是( )
| A. | 了解重庆市空气质量情况 | B. | 了解长江水流的污染情况 | ||
| C. | 了解重庆市居民的环保意识 | D. | 了解全班同学每周体育锻炼的时间 |
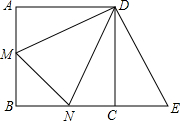 已知正方形ABCD中,M,N分别是AB,BC上的点,∠MDN=45°,延长BC至E,CE=AM,连接DE,MN,求证:NE=MN.
已知正方形ABCD中,M,N分别是AB,BC上的点,∠MDN=45°,延长BC至E,CE=AM,连接DE,MN,求证:NE=MN. ÷
÷ ,其中
,其中 .
.