题目内容
观察一列数1,3,32,33…3n发现从第二项开始,每一项与前一项之比是一个常数,像这样的数列叫做等比数列
(1)如果欲求1+3+32+33+…+320的值,可令S=1+3+32+33+…+320①
将①式两边都乘以3,得 .由②-①,可求得:S= .
(2)若数列a1,a2,a3,…,an,从第二项开始,每一项与前一项之比的常数为q,则an= (用含a1,q,n的代数式表示),如果这个常数q≠1,那么运用(1)的方法计算a1+a2+a3+…+an(用含a1,q,n的代数式表示)
(1)如果欲求1+3+32+33+…+320的值,可令S=1+3+32+33+…+320①
将①式两边都乘以3,得
(2)若数列a1,a2,a3,…,an,从第二项开始,每一项与前一项之比的常数为q,则an=
考点:规律型:数字的变化类
专题:
分析:(1)根据题中的提示和所给出的数据,可直接得出答案;
(2)由(1)的方法,依次可以推出a1+a2+a3+…+an的值,注意分两种情况讨论,从而得出答案.
(2)由(1)的方法,依次可以推出a1+a2+a3+…+an的值,注意分两种情况讨论,从而得出答案.
解答:解:(1)令s=1+3+32+33+…+320,
3S=3+32+33+34+…+321,
3S-S=321-1,
S=
(321-1);
故答案为:3s=3+32+33+34+…+321,
(321-1);
(2)∵第二项开始每一项与前一项之比的常数为q,
∴an=a1qn-1,
∵Sn=a1+a2+a3+…+an=a1+a1q+a1q2+…+a1qn-1 ①,
∴qSn=a1q+a1q2+a1q3+…+a1qn ②,
②-①得:Sn=
.
故答案为:a1qn-1.
3S=3+32+33+34+…+321,
3S-S=321-1,
S=
| 1 |
| 2 |
故答案为:3s=3+32+33+34+…+321,
| 1 |
| 2 |
(2)∵第二项开始每一项与前一项之比的常数为q,
∴an=a1qn-1,
∵Sn=a1+a2+a3+…+an=a1+a1q+a1q2+…+a1qn-1 ①,
∴qSn=a1q+a1q2+a1q3+…+a1qn ②,
②-①得:Sn=
| a1(qn-1) |
| q-1 |
故答案为:a1qn-1.
点评:此题考查了数字的变化类,是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
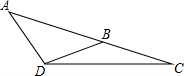 如图,在△ABC中,AD=BD=BC,若∠C=25°,则∠ADB的度数是( )
如图,在△ABC中,AD=BD=BC,若∠C=25°,则∠ADB的度数是( )| A、50° | B、60° |
| C、80° | D、90° |
 如图,在△ABC中,AB=AC,CD是∠ACB的角平分线,DE∥BC,交AC于点E,且∠CDE=25°,求∠A,∠B的度数.
如图,在△ABC中,AB=AC,CD是∠ACB的角平分线,DE∥BC,交AC于点E,且∠CDE=25°,求∠A,∠B的度数.