题目内容
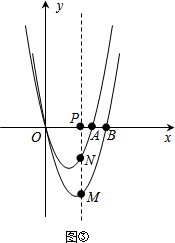
动点P在Rt△ABC的斜边AB上移动,图(2)表示动点P到两直角边的距离y与x之间的函数图象,则满足“y>2x”的x取值范围是( )


A、0≤x<
| ||
B、0≤x<
| ||
| C、0≤x<2 | ||
| D、0≤x<3 |
考点:动点问题的函数图象
专题:
分析:设y=kx+b(k≠0),利用待定系数法求出一次函数解析式,然后根据y>2x列出不等式,求解即可.
解答:解:设y=kx+b(k≠0),
由图(2)可知x=1时,y=5,x=2时,y=2,
所以,
,
解得
,
所以,y=-3x+8,
∵y>2x,
∴-3x+8>2x,
解得x<
,
又∵x为点P到BC的距离,
∴x≥0,
∴0≤x<
.
故选A.
由图(2)可知x=1时,y=5,x=2时,y=2,
所以,
|
解得
|
所以,y=-3x+8,
∵y>2x,
∴-3x+8>2x,
解得x<
| 8 |
| 5 |
又∵x为点P到BC的距离,
∴x≥0,
∴0≤x<
| 8 |
| 5 |
故选A.
点评:本题考查了动点问题函数图象,主要利用了待定系数法求一次函数解析式,解不等式,读懂题目信息并从图(2)获取信息,然后求出y与x的关系式是解题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
将抛物线y=2x2向上平移3个单位长度,再向右平移4个单位长度得到的抛物线是( )
| A、y=2(x+4)2+3 |
| B、y=2(x-4)2+3 |
| C、y=2(x+4)2-3 |
| D、y=2(x-4)2-3 |
在函数y=
中自变量x的取值范围是( )
| 1-3x |
A、x≤
| ||
B、x<
| ||
C、x≥
| ||
D、x≠
|
已知(ax•ay)5=a20 (a>0,且a≠1),那么x、y应满足( )
| A、x+y=15 | ||
| B、xy=4 | ||
| C、x+y=4 | ||
D、y=
|
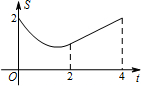
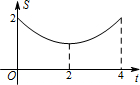
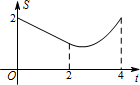
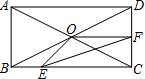 如图,在矩形ABCD中,AB=2cm,BC=4cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度分别沿B→C,C→D运动,点F运动到点D时停止,点E运动到点C时停止.设运动时间为t(单位:s),△OEF的面积为S(单位:cm2),则S与t的函数关系可用图象表示为( )
如图,在矩形ABCD中,AB=2cm,BC=4cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度分别沿B→C,C→D运动,点F运动到点D时停止,点E运动到点C时停止.设运动时间为t(单位:s),△OEF的面积为S(单位:cm2),则S与t的函数关系可用图象表示为( )