Question

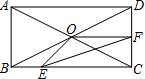如图，在矩形ABCD中，AB=2cm，BC=4cm，对角线AC，BD相交于点O，点E，F分别从B，C两点同时出发，以1cm/s的速度分别沿B→C，C→D运动，点F运动到点D时停止，点E运动到点C时停止．设运动时间为t（单位：s），△OEF的面积为S（单位：cm²），则S与t的函数关系可用图象表示为（　　）

• A、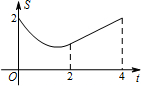
• B、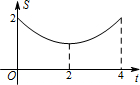
• C、
• D、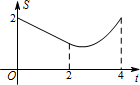

Answer 1

考点：动点问题的函数图象

专题：

分析：表示出BE、CE、CF、DF，再根据矩形的对角线互相平分且相等求出点O到BC、CD的距离，然后分①0≤x≤2时，△OEF的面积为S=S_△BCD-S_△OBE-S_△CEF-S_△ODF列式整理得到S与t的关系式，②2＜t≤4时，△OEF的面积为S=S_△BCD-S_△OBE-S_△CEF列式整理得到S与t的关系式，从而得解．

解答：解：∵在矩形ABCD中，AB=2cm，
∴CD=AB=2cm，
∵点E、点F的速度都是1cm/s，
∴BE=t、CE=4-t、CF=t、DF=2-t，
∵O是对角线AC、BD的交点，
∴点O到BC的距离是1，到CD的距离是2，
①0≤x≤2时，
△OEF的面积为S=S_△BCD-S_△OBE-S_△CEF-S_△ODF
=

1

2

×4×2-

1

2

t•1-

1

2

（4-t）•t-

1

2

（2-t）•2
=4-

1

2

t-2t+

1

2

t²-2+t
=

1

2

t²-

3

2

t+2，
②2＜t≤4时，
△OEF的面积为S=S_△BCD-S_△OBE-S_△CEF
=

1

2

×4×2-

1

2

t•1-

1

2

（4-t）•2
=4-

1

2

t-4+t
=

1

2

t，
纵观各选项，只有A选项图形符合．
故选A．

点评：本题考查了动点问题函数图象，读懂题目信息，根据点E、F的位置的不同分两种情况表示出△OEF的面积是解题的关键．