题目内容
如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,点E、F同时从点C出发,以
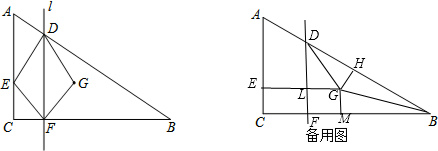
cm/s的速度分别沿CA、CB匀速运动,当点E到达点 A时,两点同时停止运动,设运动时间为ts.过点F作BC的垂线l交AB于点D,点G与点E关于直线l对称.

(1)当t= s时,点G在∠ABC的平分线上;
(2)当t= s时,点G在AB边上;
(3)设△DFG与△DFB重合部分的面积为Scm2,求S与t之间的函数关系式,并写出t的取值范围.
| 1 |
| 2 |

(1)当t=
(2)当t=
(3)设△DFG与△DFB重合部分的面积为Scm2,求S与t之间的函数关系式,并写出t的取值范围.
考点:相似形综合题
专题:
分析:(1)过点G做GH⊥BD,垂足为H,GM⊥FB,垂足为M,点E、F同时从点C出发,所以EC=CF=FM=GM=GH=
t,且DG也是△BDF的角平分线,由△BDF∽△ABC得:
=
=
,∴BD=5-
t,DF=3-
t,可求得DL、BM的长度,由DL=DH,BH=BM,构造关于t的方程可以求得答案.
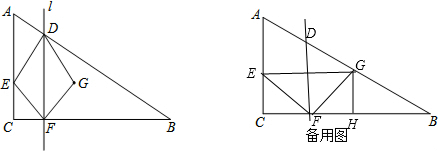
(2)点G在AB边上时,过点G作GH⊥BC,垂足为H,由(1)中的数值,结合△BGH∽△BAC,构造出关于t的方程,可以得到答案.
(3))由DF∥AC得到△ABC∽△DBF,∴
=
,即
=
,得到DF=
(8-t),分两种情况讨论:
①当0<t≤
时,S=S△DFG=S△DEF=
DF•CF=
×
(8-t)×
t=-
t2+
t;
②当
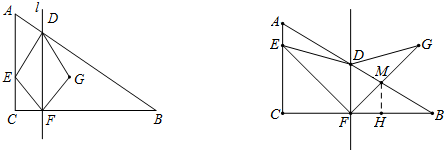
<t≤6时,设FG交AB于点M,过点M作MH⊥BC于H,设FH=MH=a,求得BH,解出a与t的关系,继而求得S与t的关系.
| 1 |
| 2 |
| BD |
| BA |
| BF |
| CB |
| DF |
| AC |
| 5 |
| 8 |
| 3 |
| 8 |
(2)点G在AB边上时,过点G作GH⊥BC,垂足为H,由(1)中的数值,结合△BGH∽△BAC,构造出关于t的方程,可以得到答案.
(3))由DF∥AC得到△ABC∽△DBF,∴
| DF |
| AC |
| BF |
| BC |
| DF |
| 3 |
4-
| ||
| 4 |
| 3 |
| 8 |
①当0<t≤
| 12 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
| 1 |
| 2 |
| 3 |
| 32 |
| 3 |
| 4 |
②当
| 12 |
| 5 |
解答:解:(1)
过点G做GH⊥BD,垂足为H,GM⊥FB,
垂足为M,点E、F同时从点C出发,所以四边形ECFL、四边形LFGM都是正方形,
∴EC=CF=FM=GM=GH=
t,
又∵DG也是△BDF的角平分线,
∴DL=DH,
∵DF∥AC,
∴△BDF∽△ABC
∴
=
=
,
∴BD=5-
t,DF=3-
t,
又∵DL=DH=3-
t-
t=3-
t,
BH=BM=4-t,又∵BD=BH+HD,
∴5-
t=3-
t+4-t,解得:t=
.
(2)
点G在AB边上时,过点G作GH⊥BC,垂足为H,
∵GH∥AC,
所以△BGH∽△BAC,
∴
=
,
即:
=
,
解得:t=
.
(3)∵DF∥AC,
∴△ABC∽△DBF,
∴
=
,
即
=
,
解得DF=
(8-t)
①当0<t≤
时,S=S△DFG=S△DEF=
DF•CF=
×
(8-t)×
t=-
t2+
t.
②当
<t≤6时,设FG交AB于点M,过点M作MH⊥BC于H,设FH=MH=a,
则BH=
a,
∴
t+a+
a=4,
解得a=
(8-t),
S=S△DFM=
DF•FH=
×
(8-t)×
(8-t)=
(8-t)2.
| 8 |
| 5 |
过点G做GH⊥BD,垂足为H,GM⊥FB,
垂足为M,点E、F同时从点C出发,所以四边形ECFL、四边形LFGM都是正方形,
∴EC=CF=FM=GM=GH=
| 1 |
| 2 |
又∵DG也是△BDF的角平分线,
∴DL=DH,
∵DF∥AC,
∴△BDF∽△ABC
∴
| BD |
| BA |
| BF |
| CB |
| DF |
| AC |
∴BD=5-
| 5 |
| 8 |
| 3 |
| 8 |
又∵DL=DH=3-
| 3 |
| 8 |
| 1 |
| 2 |
| 7 |
| 8 |
BH=BM=4-t,又∵BD=BH+HD,
∴5-
| 5 |
| 8 |
| 7 |
| 8 |
| 8 |
| 5 |

(2)
| 12 |
| 5 |
点G在AB边上时,过点G作GH⊥BC,垂足为H,
∵GH∥AC,
所以△BGH∽△BAC,
∴
| BH |
| BC |
| GH |
| AC |
即:
| 4-t |
| 4 |
| ||
| 3 |
解得:t=
| 12 |
| 5 |

(3)∵DF∥AC,
∴△ABC∽△DBF,
∴
| DF |
| AC |
| BF |
| BC |
即
| DF |
| 3 |
4-
| ||
| 4 |
解得DF=
| 3 |
| 8 |
①当0<t≤
| 12 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
| 1 |
| 2 |
| 3 |
| 32 |
| 3 |
| 4 |
②当
| 12 |
| 5 |
则BH=
| 4 |
| 3 |
∴
| 1 |
| 2 |
| 4 |
| 3 |
解得a=
| 3 |
| 14 |
S=S△DFM=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
| 3 |
| 14 |
| 9 |
| 224 |

点评:本题考查了三角形相似的判定与性质的综合应用,学会分类讨论的思想和用方程思想解几何题是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
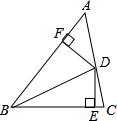 如图,∠ABC=60°,点D在AC上,BD=16,DE⊥BC,DF⊥AB,且DE=DF,求:
如图,∠ABC=60°,点D在AC上,BD=16,DE⊥BC,DF⊥AB,且DE=DF,求: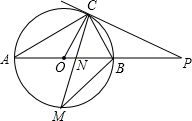 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,连AC、OC,若AC=PC,∠P=30°.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,连AC、OC,若AC=PC,∠P=30°.
 如图,在△ABC中,AB的垂直平分线MN交AB于点D,交AC于点E,且AC=15cm,△BCD的周长等于25cm.
如图,在△ABC中,AB的垂直平分线MN交AB于点D,交AC于点E,且AC=15cm,△BCD的周长等于25cm. 如图,在?ABCD中,E为CD上的一点,若S△AED:S△BCE=4:1,则S△AED:S△ABE=
如图,在?ABCD中,E为CD上的一点,若S△AED:S△BCE=4:1,则S△AED:S△ABE=