题目内容
已知点（-1，3），（3，3）在抛物线y=ax2+bx+c上，则抛物线的对称轴方程是（ ）
A、x=-
| ||
| B、x=2 | ||
| C、x=3 | ||
| D、x=1 |
考点：二次函数图象上点的坐标特征
专题：
分析：根据两已知点的特征得到点（-1，3）和点（3，3）是抛物线y=ax2+bx+c上的对称点，所以求出这两点的对称轴即可．
解答：解：∵点（-1，3）和（3，3）在抛物线y=ax2+bx+c上，
而点（-1，3）与（3，3）的纵坐标相等，
∴点（-1，3）和点（3，3）是抛物线y=ax2+bx+c上的对称点，
∴抛物线的对称轴为直线x=1．
故选D．
而点（-1，3）与（3，3）的纵坐标相等，
∴点（-1，3）和点（3，3）是抛物线y=ax2+bx+c上的对称点，
∴抛物线的对称轴为直线x=1．
故选D．
点评：本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．也考查了二次函数的性质．
练习册系列答案
相关题目
下面的结论中错误的是（ ）
| A、到已知角的两边的距离相等的点在同一直线上 |
| B、若直线上有一点到已知角的两边的距离相等，则这条直线平分已知角 |
| C、角的内部到角的两边距离相等的某点与角的顶点的连线平分已知角 |
| D、角的内部有两点各自到角的两边的距离相等，经过这两点的直线平分已知角 |
下列判断正确的是（ ）
| A、若|-a|＜|-b|，则a＞b |
| B、若a＞0，且（1-b）a＜0，则b＜1 |
| C、若a≠b，则a2一定不等于b2 |
| D、若a＜0，则2a＜a |
一个三角形的3个外角度数之比为2：3：3，则这个三角形为（ ）
| A、等腰直角三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等边三角形 |
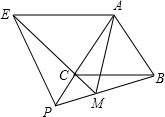如图已知△ABC为等边三角形，P是AC延长线上一点，PA为边作等边三角形APE，EC的延长线交BP于点M，连接AM．求证：